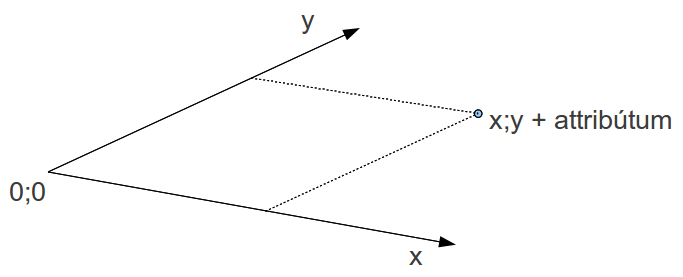
A szokásos térképek és egyéb térképi ábrázolások általában két dimenziósak (2D). Ez azt jelenti, hogy az ábrázolt terület minden egyes pontjának térképi helyét egyértelműen meghatározza két térdimenzió, például a földrajzi szélesség és a földrajzi hosszúság értéke. Ezen kívül minden egyes ábrázolt ponthoz rendelünk még legalább egy szakadatot (attribútum adatot) is (14.1. ábra). Ez utóbbi adat az, amelynek értékét ábrázolja a térkép. Így például, domborzati térképek esetében minden ponthoz rendelünk két koordinátát, szakadatként pedig az adott pont tengerszint feletti magasságát és ennek aktuális értéke határozza meg az adott pont színét: minél alacsonyabb, annál zöldebb és minél magasabb, annál sötétebb barna (14.2. ábra). Ha ezt az adatbázist (mert hiszen minden térkép végül is felfogható egy adatbázisként. Ne feledjük, hogy az adatbázis fogalom nem egyenlő az adattáblával!) úgy ábrázolnánk, hogy az egyes pontok látszó helyét a magasságuk szerint módosítanánk, akkor egy szemléletes, mondhatni “térbeli” képét kapnánk a területnek (14.3. ábra). Igen gyakran ezt a megjelenítési módot nevezik - hibásan! - 3D-nek. A bemutatott eljárással csak úgynevezett “2,5D” modellhez jutunk. Ez az elnevezés persze matematikai szempontból hibás, de nem is ez a lényeg: arra céloz csupán, hogy valójában ez egy speciálisan megrajzolt 2D modell, amely így 3D hatást nyújt. Így, minthogy félúton van a 3D és a 2D modell között, általában 2,5D-nek nevezzük.

14.1. ábra - A kétdimenziós modell

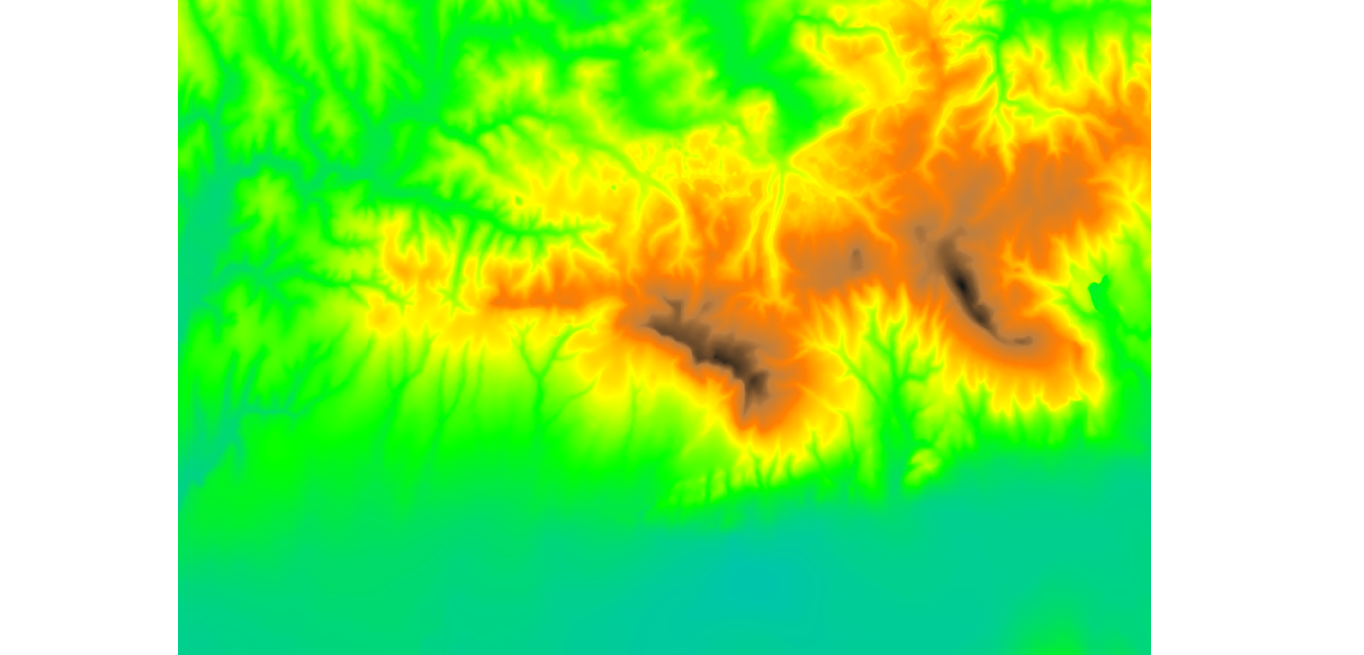
14.2. ábra - Kétdimenziós terepmodell – a hagyományos domborzati térkép. A Mecsek nyugati- és középső része a Pécsi-síksággal

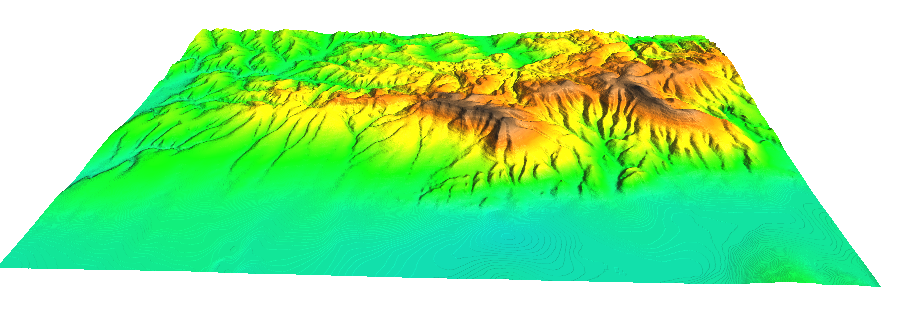
14.3. ábra - Három dimenziós látszati kép 2 dimenziós térképből: 2,5D modell. Kétszeres túlmagasítással, 5500 méter magasból, délkeleti megvilágításban, délről szemlélve a 2. ábrán látható területet (video)

A valós 3D modell olyan, hogy minden egyes pontjához három térdimenzió tartozik és egy szakadat: például, földrajzi szélesség és hosszúság, tengerszint feletti magasság, kőzet neve. Fontos különbség tehát, hogy nem attól lesz valami 3D modell, hogy attribútum-adatként a magasságot tartalmazza, hanem attól, hogy minden pontját három térbeli koordináta írja le és e mellett még minden ponthoz rendelünk egy szakadatot is (14.4. ábra). Mivel a 14.2. ábrán bemutatott modell esetében ez nem teljesülhet, az nem is lehet 3D. Valós 3D modellre példa az 14.5. ábrán látható modell.

14.4. ábra - A három dimenziós modell

14.5. ábra - Példa a valós 3D-re. Egy felszín alatti tömeg elhelyezkedése a GRASS-ban megjelenítve (forrás)