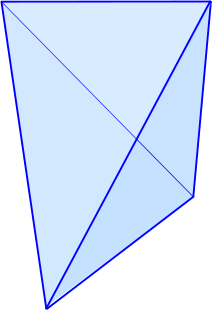
Vektor alapú valós 3D modellek is felépíthetőek, ebben az esetben tetrahedronokból álló rendszer modellezi a valóságos térfogatot. A tetrahedron olyan négyoldalú test, amelynek oldalai háromszögek (14.14. ábra). A voxelekhez hasonlóan ezekből is felépíthető olyan struktúra, amelyik folytonosan és átfedés mentesen tölti ki a modellezendő teret (14.15. ábra).

A tetrahedronokból álló struktúra a TIN-nel mutat rokonságot: az egyes elemekhez több szakadat is rendelhető, mert vektoros elemek és így a hozzájuk kapcsolt adattábla mindegyikre vonatkozóan több mezőt (tehát attribútumot) is tartalmazhat. Elkészítése hasonló a síkbeli Delaunay-háromszögekéhez, itt azonban körök helyett gömböket kell használni és a gömb felületére illeszkedő pontokat kell megkeresni.

A tetrahedronokból álló térfogat kívülről alapesetben ugyanúgy átlátszatlan, mint a voxelekből való, ezért ugyanúgy szükséges lehet a metszése. A tetrahedron alapú modell metszete 2D vektoros modell, amelyben a metszés három- vagy négyoldalú, szabálytalanul elhelyezkedő poligonokból épül fel (14.16. ábra).

14.14. ábra - A tetrahedron. Megfigyelhető, hogy mindegyik oldala egy-egy háromszög

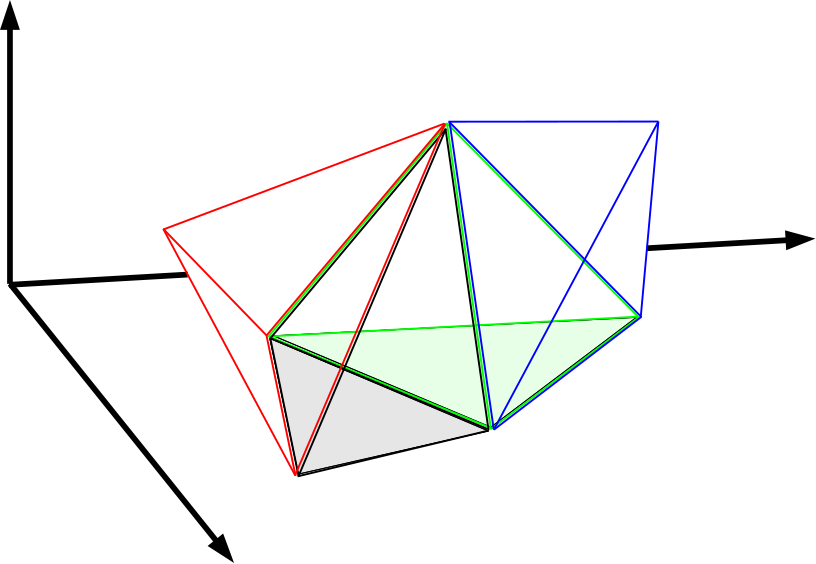
14.15. ábra - Térfogat kitöltése tetrahedronokkal. Négy, külöbőző színű tetrahedron tölti ki vonatkozó teret. A tájékozódást segíti a háttérben levő 3D koordinátarendszer tengelyeinek feltüntetése és az, hogy a képzeletbeli alapsíkra felfekvő részeket halvány színezés jelöli. A kék test ugyanaz, mint a 14.14. ábrán látható.

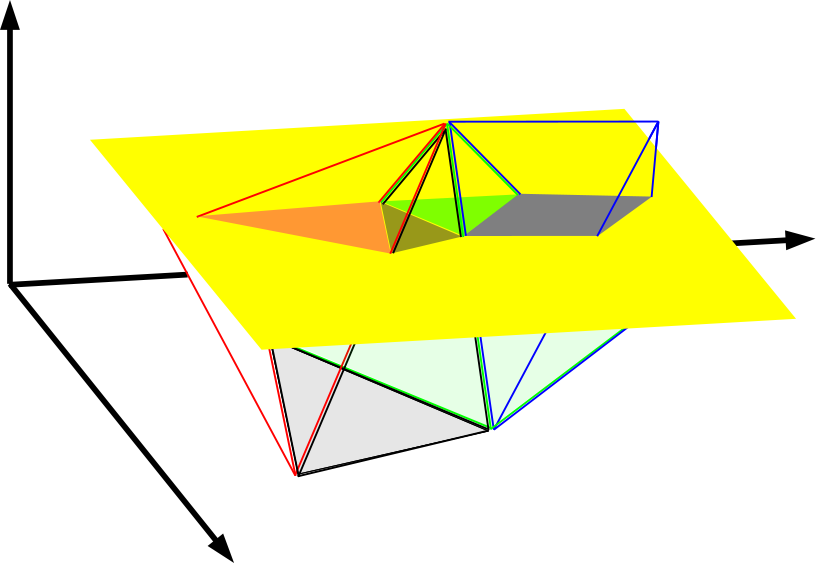
14.16. ábra - A 14.15. ábra tetrahedronjai síkkal elmetszve. A sík (sárga) párhuzamos az alappal, amin a tetrahedronok felfekszenek. Megfigyelhető, hogy a metszés eredménye négy poligon, melyek három vagy négy oldalúak. A poligonok színezése ugyanaz, mint a tetrahedroné, amelynek a metszésével előálltak.