Valódi 3D modelleket leginkább bányák, barlangok, földtani és légköri jelenségek vizsgálatához használnak, de nem nélkülözhető a vastagabb víztömegek (tengerek, tavak) viselkedésének modellezésekor sem.
Míg az általános célú térinformatikai rendszerek általában képesek a 2,5D modellek kezelésére és azok elemzésére, addig valódi 3D-t már csak néhány professzionális GIS kezel és persze az egy-egy adott igény kielégítésére képes célszoftverek (pl.: légköri modellező környezetek).[1].
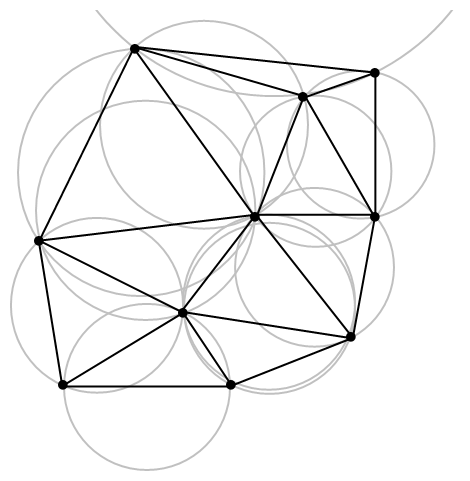
A 2,5D modellek között raszteres és vektoros felépítésűek is találhatóak. A 2,5D raszteres modellek a megszokott raszteres modellekkel teljes mértékben megegyeznek. A vektoros 2,5D modellek sajátossága, hogy általában úgynevezett TIN szerkezetűek. A TIN (Triangulated irregular network – szabálytalan háromszög hálózat) olyan, az ábrázolandó felszínt folytonosan és átfedés mentesen különböző háromszögek építik fel. Az egyes háromszögek síkja egymáshoz képest szöget zárhat be. Minél kisebbek a háromszögek, annál pontosabban lehet ezzel az eljárással modellezni a felszínt.[2] A TIN készítésének alapja a Delaunay-háromszögelés. Ezen eljárás alapja igen vázlatosan az, hogy minden egyes pontra egy olyan kört illesztünk, mely másik két pontra is illeszkedik és megköveteljük, hogy e kör területe minimális legyen. E három pontot ezután összekötjük egymással, vagyis létrehozunk egy háromszöget. Az eljárást addig ismételjük, míg mindegyik pontot össze nem kötöttük két másikkal (14.6. ábra).
Ezen eljárás nagyon szerencsés tulajdonsága, hogy nem alakulnak ki olyan háromszögek, amelyek nagyon keskenyek és hosszúak lennének, így TIN-ként használva jól közelítik a valós felszínt.
Az elkészült háromszögháló csomópontjai az eredeti pontokkal egyeznek meg, az azokat összekötő élek pedig a Delaunay-háromszögek. Az élek olyanok, hogy egy attribútumtáblából mindegyikükhöz tartozik egy maximum és egy minimum érték is, így már 3D látszati kép készülhet belőlük.
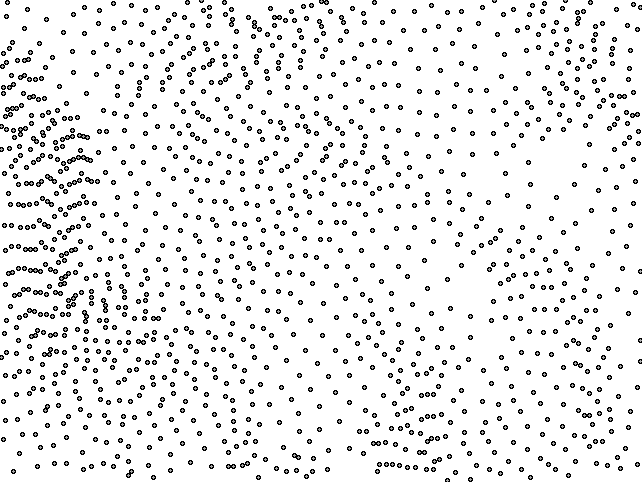
Ezt az eljárást használjuk például akkor, amikor valamilyen forrásból csak pontszerű értékek (például magassági értékek) állnak rendelkezésre (14.7. ábra). Ebből a pontfelhőből készíti el a szoftver a Delaunay-háromszögeket, vagyis a TIN-t. Ez még csak kétdimenziós, mert bár az egyes élekhez már tartozik minimum és maximum magassági érték is, de a monitoron mégy csak egyszerű háromszög hálózatnak látszik (14.8. ábra).
A 3D látszati képet (vagyis a 2,5D modellt) általában a térinformatikai szoftver egy következő lépésben (és általában egy külön modullal) készíti el (14.9. ábra).
14.8. ábra - A 14.7. ábra pontjaira illesztett Delaunay-háromszögek. Síkbeli kép, noha a hálózat ritkulása és sűrűsödése már mutatja a domborzatot is.
 |
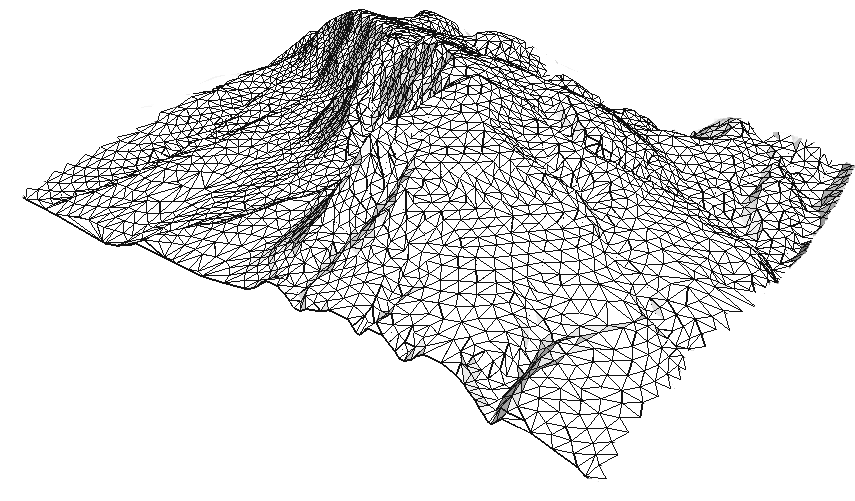
14.9. ábra - A 14.7. ábrán látható magassági pontok alapján, a 14.8. ábra Delaunay-háromszögeiből készült 3D látszati kép. Az ábrázolt terület nagyobb, mint az ábrák területe. A Jakab-hegy a Mecsekben, 3-szoros túlmagasítással, dél-keletről.
 |
[1] A “hagyományos”, kereskedelmi szoftverekhez (ArcGIS, Mapinfo stb.) általában (kiegészítő csomagban) megvásárolható valamilyen 3D modellező. A GRASS, a vezető térinformatikai célú szabad szoftver alapértelmezésben képes valódi 3D modellek kezelésére.
[2] Érdekességként megemlíthető, hogy a számítógépes játékok zöme ezzel az eljárással hozza létre a – virtuális – tájképet, és nem véletlen, hogy a grafikus processzorok teljesítményét is gyakran jellemzik azzal, hogy mennyi háromszöget képesek egy másodpec alatt kiszámolni.