A múlt század húszas éveiben a svéd kormány támogatta azokat a gazdákat, akik az addig szokásos, korlátozások nélküli legeltetési módszert (amellyel pl. a marhagulyák károkat okoztak a friss erdőtelepítésekben) fölváltották intenzívebb legelőhasználati módszerekkel. Ennek lényege az volt, hogy elkerített és feljavított legelőkre korlátozták az állatok mozgását, így védve a facsemetéket és egyéb mezőgazdasági területeket.
Hägerstrand először egy általános, elméleti térbeli diffúziós modellt készített (Haggett, 2006), majd a fenti problémára szimulációk futtatásával alkalmazta.
Hägerstrand feltételezte, hogy az információ a forrástól, akit nevezzünk feladónak, az üzenet átvevőjéhez közvetlen, szóbeli kommunikációval jut el (személyes, vagy telefonon történt megbeszélés során). Az információ átadásának valószínűsége a távolsággal exponenciálisan csökken (11.4. ábra). A sztochasztikus modell legfontosabb alapszabályai a következők (részletesebben lásd: Haggett, 2006):
1.A vizsgált területet 5x5 km2-es cellákra osztotta, amelyekben cellánként egy ember helyezkedik el.
2.Az információ átvételével egy időben megtörténik az innováció elfogadása.
3.Minden egyes iteráció során egy üzenetet közvetít a feladó attól függetlenül, hogy az átvevő rendelkezik-e már az információval, vagy sem.
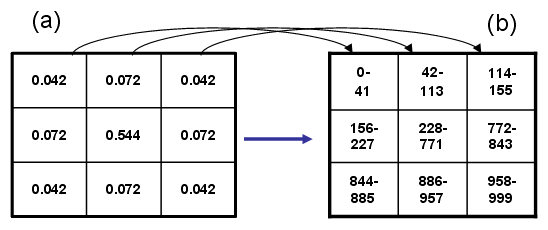
Az információk átadásának valószínűségét az ú.n. MIF-ek (átlaginformációs mezők) szabályozzák. A cellák (11.5. (a) ábra) tartalmazzák a valószínűségek értékeit (a mezővel lefedett területen kívül a valószínűség 0) és az ezek alapján generált kumulatív valószínűségeket (11.5. (b) ábra). A mezők számításának módszerét az 11.6. ábra animációjának segítségével tanulmányozhatjuk.
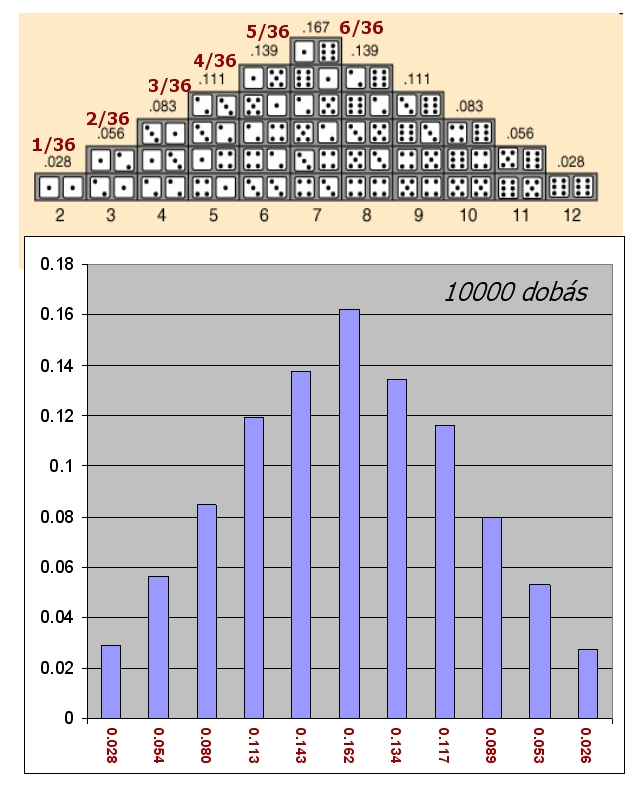
A szimuláció folyamata bármikor megállítható, viszont ha már minden egyes cellába eljutott az üzenet, akkor a diffúziós folyamat leáll. Nagyszámú (több száz, akár több ezer) szimulációs sorozat - amelyeket realizációknak nevezünk - lefuttatása minden esetben kissé eltérő térbeli mintázatot ad, de összegük a kiindulási valószínűségeket adja vissza (ld. Kockadobás, ismert kiindulási valószínűség esetén 11.4. ábra).
A tudomány történetében az első, Monte Carlo szimuláció elvén nyugvó, a π szám értékének meghatározására elvégzett Buffon tűje kísérletet tekinthetjük.
Számítógéppel a II. Világháború alatt a Manhattan program keretében Teller Ede és munkatársai végeztek sztochasztikus szimulációkat az atombomba előállításához nélkülözhetetlen neutron diffúzió vizsgálatára. Az elnevezés is a csoport egyik tagjától ered, aki rajongott a szerencsejátékokért (11.4. ábra). A sztochasztikus szimulációs módszereket Monte Carlo szimulációknak is szokták nevezni, melynek alapjait Neumann János magyar származású matematikus dolgozta ki. A sztochasztikus rendszerek sajátosságait az 1. fejezetben ismertettük. Ebben az esetben is a vizsgált rendszert egy fekete doboznak tekinthetjük, amelyen belül az információ terjedését véletlen események sorozataként kezeljük.