Hägerstrand alapmodellje nagyon sok egyszerűsítést tartalmaz. Valós folyamatok szimulációs modellezéséhez a szabályok módosítására van szükség. A módosítások egy része csak a cellák szerkezetét érinti: a cellák alakja, elrendezése a lefedett valós terület ismeretében egyszerűen változtatható, pl. hatszög alakú cellák alkalmazása. Egy terület „méhsejt”-ekkel történt lefedésére példa a MÉTA program alaptérképe.Kissé összetettebb, bár számítógéppel könnyen megoldható átalakítása az alapmodellnek, amikor a az egyes cellákhoz tartozó népesség-, vagy egyedszámot alakítjuk a valóságnak megfelelően. További átalakítást jelent, ha a modellbe határokat és korlátokat építünk be, amelyek a diffúziós folyamatok akadályaiként funkcionálnak (ld. Haggett, 2006). Ezen változtatások megvalósításához a geoinformatika (GIS) számos megoldási lehetőséget kínál.
Tanulmányozzuk az 7. ábrát, amely a középkori pestisjárvány európai elterjedését ábrázolja! Választ kaphatunk a következő kérdésekre: mely központokból, milyen irányban és milyen átlagos sebességgel terjedt a halálos kór (Röst, 2010)?
SIR modell
A járványterjedés térbeli modellezésére alkalmas az ú.n. Eden modell módosítása (amelynek egy tumornövekedésre kidolgozott változata a következő interaktív animáción tanulmányozható (forrás).
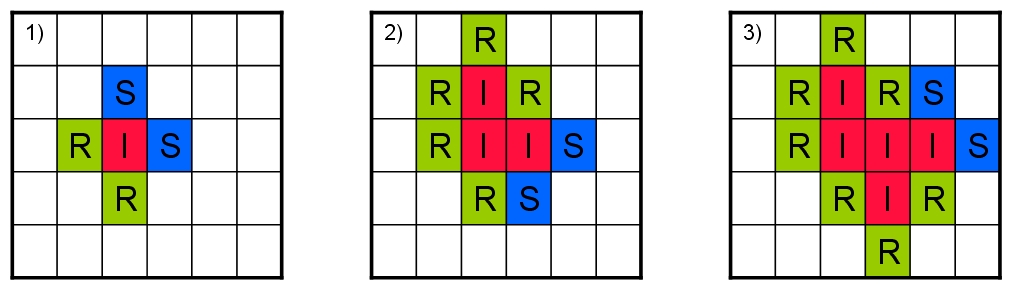
Az alapmodellen (használjuk újra Hägerstrand alapmodelljét!) módosításokat kell végrehajtanunk (Kun, 2011). Jelölje I (Infected: fertőzőtt), S (Susceptible: fogékony) és R (Recovered: gyógyult) az egymástól megkülönböztetett személyek csoportjait. A vírusterjedést újra egy rácsmodellben ábrázoljuk: minden mezőben egy ember helyezkedik el. A folyamat egy I fertőzőtt egyedtől indul, aki a vele közvetlenül érintkező szomszédjának adja át a fertőzést, amennyiben a szomszéd az S csoportba tartozik. A gyógyult egyedek irányába nyilvánvalóan nem terjedhet a fertőzés (11.8. ábra). Amennyiben az I fertőzött egyed p valószínűséggel adja tovább a fertőzést, 1-p a valószínűsége, hogy a közvetlen szomszéd immunis. A beteg egyedek által alkotott mintázat összefüggő és a mintázat, valamint a betegségterjedés jellemzői a p értéktől függnek. Létezik olyan pc kritikus érték, amely alatt a fertőződés néhány lépés után megáll, felette pedig a járvány elindul. A p= pc esetet a 9. fejezetben, a fraktálmintázatok vizsgálata során már tárgyaltuk.
11.8. ábra - A járványterjedési modell algoritmusa. (1) A fertőzőtt egyedet a piros szín jelöli. A betegség a vele közvetlenül érintkező két kékkel jelölt egyedre terjedhet tovább. Két szomszéd immunis. (2) Két további egyed megbetegedett, öt szomszéd viszont immunisnak bizonyult. További két beteg egyed fertőzőképes, a betegség a kékkel jelölt egyedekre terjedhet tovább. (3) Öt beteg egyed van, amelyeket az immunisak szinte teljesen körbezárnak. A terjedés további irányai a két kék egyed felé mutatnak.
 |
A vízben oldható szennyezőanyagok terjedésének egyik alapvető folyamata a szennyezőanyag térbeli szóródása. A szóródás kémiai folyamata a különböző koncentrációjú oldatok között a részecskék diffúziós mozgása, amely a koncentráció-különbség kiegyenlítődéséig tart. A folyamatot Fick I. törvénye írja le (Kovács, 2004). Talajvízben oldott szennyeződés esetén a diffúzió csak akkor meghatározó folyamat, ha a szivárgás sebessége kicsi (11.9. ábra). Áramló talajvízben a hidrodinamikai transzportfolyamatok határozzák meg a szennyezőanyagok szóródását, hatásuk mellett a diffúziós anyagáram szerepe elhanyagolható.
Valamely szennyezőanyag porózus közegbeli szóródása diffúzió hatására véletlen jellegű, sztochasztikus folyamat. A teljes szennyezőanyag-tömeget kisebb egységekre bontják, majd a részecskék sztochasztikus mozgásait a „véletlen bolyongás” (ld. Brown-mozgás interaktív szimulációja) módszerével szimulálják (Monte Carlo szimuláció, forrás).
