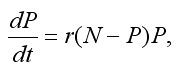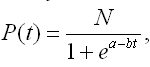Az N egyed eltartására képes környezetben a népességszám növekedést (populáció: P) a logisztikus növekedési modell írja le. Alkalmazzuk ezt a modellt az információterjedés leírására. Legyen egy N lélekszámú népességben P azon egyéneknek a száma, akik már ismerik az információt, ekkor N-P azok száma, akik nem. Feltehetjük, hogy a terjedés sebessége arányos azok számával, akik már ismerik az információt, és azokéval is, akik majd még ezután fogják megismerni.
ahol t idő, r>o állandó, a növekedési ráta: r(N-P) értékét határozza meg. A ráta értéke csökken, ahogy P közeledik N-hez. Az ú.n. egyensúlyi egyeneseket a P=0 és P=N értékeknél vannak, ezek határozzák meg a függvény alsó és felső korlátját. P=N/2-nél a görbének inflexiós pontja van (Thomas, 2006): addig egyre növekszik az információterjedés sebessége, onnantól pedig egyre inkább csökken, vagyis a folyamat lassan indul, gyorsulva eléri sebessége maximumát, majd a felső határértékhez közeledve újra lelassul (11.3. ábra).
A folyamatot leíró függvény a következő:
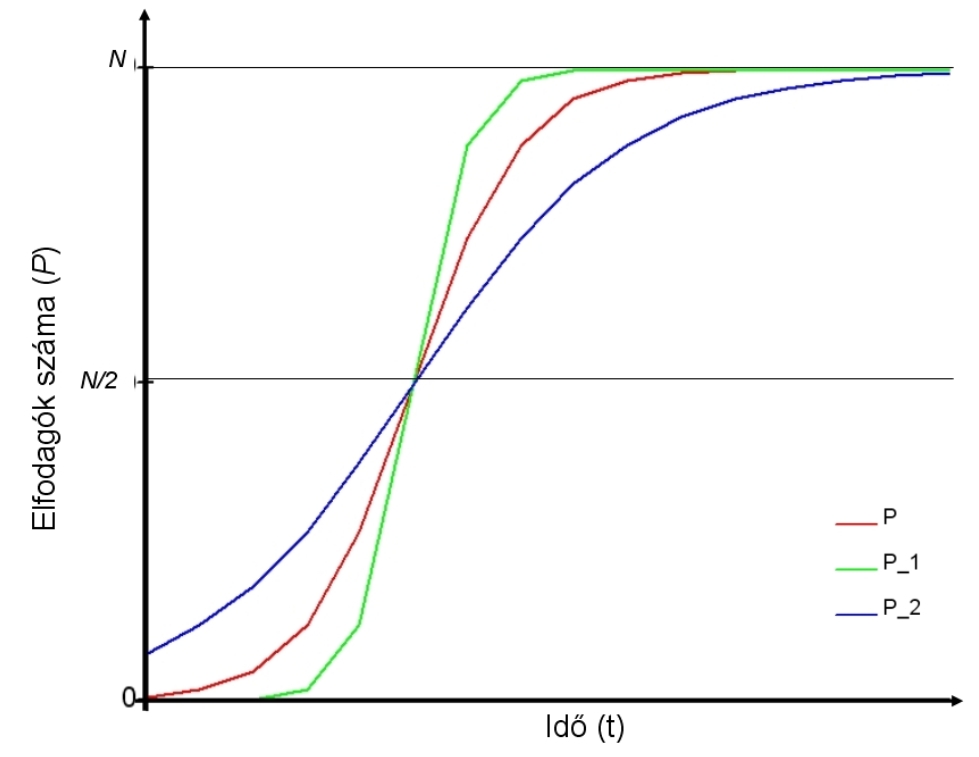
ahol P(t) az információt t idő után elfogadók száma, a konstans, b a görbe meredeksége. A b értéket az határozza meg, hogy milyen gyorsan terjed az információ, a P_1 görbe egy gyorsabb, míg a P_2 egy lassabb folyamatot leíró görbe (3. ábra).