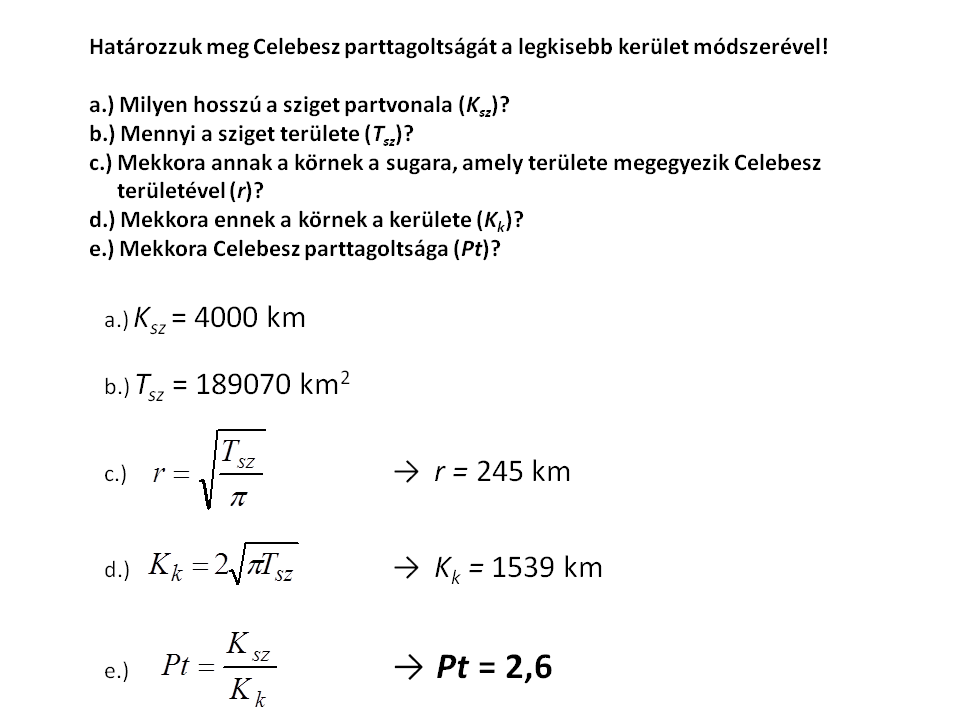Tartalom
A fejezet céljai: áttekintjük a parttagoltság meghatározásának hagyományos természetföldrajzi módszereit, majd az Angol-sziget partvonalának hosszmérésére tett kísérleteink alapján arra a következetésre jutunk, hogy ez a hossz nem határozható meg egyértelműen. A méréseinkből levezetünk egy olyan értéket, amely a természetben tapasztalt egyszerűbb és bonyolultabb formák kvantitaív jellemzésére egyaránt alkalmas, ez a fraktáldimenzió. Olyan dimenzió-számítási módszerre is látunk gyakorlati példát, amely alkalmas magasabb dimenziókban – a térben – a fraktálok vizsgálatára. elemezzük, hogy a térképeszetben és térinformatikai elemzésekben milyen szerepe lehet a fraktálokdimenziónak.
Szükséges ismeretek, fogalmak: parttagoltság, térképi hosszmérések, Steinhaus-paradoxon, legjobban illeszkedő egyenes, topológiai dimenzió
Mindenki számára ismert az a tény, hogy Norvégia partvonala tagoltabb, mint mondjuk az Ibériai-félsziget partvonala. Arra azonban már kevesebben tudnának válaszolni, hogy mi alapján mondjuk ezt. Egyik csipkézettebb, a másik kevésbé? Egyiken sok az öböl, félsziget, másikon kevesebb? A fent említett két példa esetén ez elég nyilvánvaló, de mit tudnánk mondani pl. Izland és az Angol-sziget, vagy éppen Borneó és Új-Guinea esetében? Van-e olyan módszerünk, amellyel eldönthető, illetve számszerűsíthető egy sziget, vagy akár egy földrész parttagoltsága? A módszerek sokfélesége azt mutatja, hogy igazán jó módszer nincs.
A fiktív partvonalak módszere olyan fiktív partvonalakkal hasonlítja össze a valódi partvonal hosszát, amelyeket vagy belülről, vagy kívülről rajzolunk a sziget partvonalára úgy, hogy azok kisimítsák a partvonal egyenetlenségeit (lehetőleg mindenhol konvexek legyenek). A módszer természetesen rendkívül szubjektív.
Az azonos parttávolságok módszerével mérve a sziget (vagy kontinens) területét a sziget azon részének területével hasonlítjuk össze, amelyet a parttól egy megadott távolságra futó izovonal határol körbe. Ez a megadott távolság a sziget méretétől függ, más lesz Eurázsia, Grönland és a Szentendrei-sziget esetében. Ennek meghatározására nincsen megfelelő módszer.
Nagyon egyszerűnek tűnne, ha a sziget területét és kerületét hasonlítanánk össze, a probléma csupán az, hogy két hasonló sziget esetén, ha az egyik területe kétszer akkora, mint a másiké, a parttagoltsága közel másfélszerese lenne.
A legelterjedtebb módszer a parttagoltság mérésére a legkisebb kerület módszere. A sziget parttagoltságát ekkor a sziget partvonalhosszának és a szigettel megegyező területű kör kerületének a hányadosa adja. Mivel az azonos területű síkidomok közül a körnek a legkisebb a kerülete, a parttagoltságra mindig egy egynél nagyobb értéket kapunk (szabályos kör alakú sziget esetén egyet is kaphatunk). Kontinensnyi méretekben teljesen következetesen akkor járnánk el, ha olyan gömbi kör kerületével hasonlítanánk össze a kontinens partvonalának a hosszát, amely által körülzárt gömbsüveg felülete egyezik meg a kontinens területével. Kisebb méretekben természetesen síkban is elég dolgoznunk.
Feladat: Határozzuk meg Celebesz parttagoltságát a legkisebb kerület módszerével (9.1. ábra, amimáció)! a.) Milyen hosszú a sziget partvonala (Ksz)? b.) Mennyi a sziget területe (Tsz)? c.) Mekkora annak a körnek a sugara, amely területe megegyezik Celebesz területével (r)? d.) Mekkora ennek a körnek a kerülete (Kk)? e.) Mekkora Celebesz parttagoltsága (Pt)?