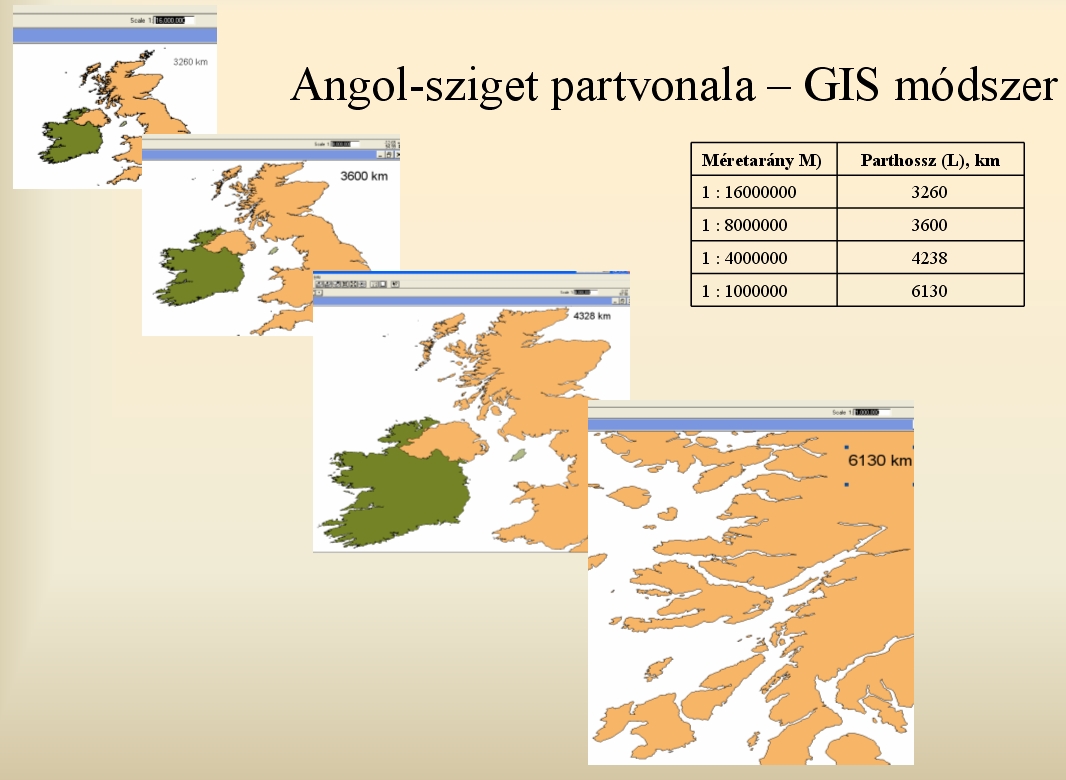
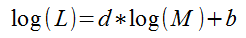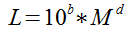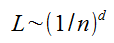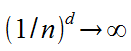Milyen hosszú a brit tengerpart? − kérdezte Benoit Mandelbrot amerikai kutató a Science tudományos folyóiratban 1967-ben megjelent cikkében. A válasz nem adható meg egyértelműen egy valamilyen (pl. km) hosszúságegységben kifejezett számértékkel. A mérés végeredménye attól függ, hogy milyen pontossággal, milyen méretarányú térképen végezzük el a hosszmérést.A mérések méretarányfüggését korábban (már a XIX. sz. végén) is többen megállapították: ha valamely természetes határvonal hosszát nagyméretarányú térképről, majd pontos műszerrel állapították meg, a hossz növekedését tapasztalták. Ezt a jelenséget nevezzük "Steinhaus paradoxon"-nak.Évmilliók tektonikus tevékenysége, a szüntelenül működő erózió és szedimentáció rendkívül csipkézetté, egyenetlenné, vagyis tagolttá formálta a partvonalat. Sorra véve az egyre nagyobb méretarányú térképlapokat egyre több részlet, kacskaringó (öböl, fok, abráziós fülke, stb.) tárulkozik föl. Mérhetünk a terepen is (1:1 méretarány), hogy a sziklák szabálytalanságait is figyelembe vegyük, vagy akár nagyítóval a kézben a kőzet ásványi alkotói közötti hézagokat is lemérhetjük. Ez a küzdelem természetesen az eredeti cél szempontjából már kilátástalan és értelmetlen is, de a kérdés jogos: miért ne mérhetnénk? Van-e megoldás, létezik-e egy olyan kvantitatív módszer, amellyel megadható egy, a partvonalat jellemző érték, léptéktől függetlenül?

Mérjük meg különböző méretarányú térképeken az Angol-sziget partvonalának hosszát (9.2. ábra)!

9.2. ábra - Angol-sziget partvonalhossza geoinformatikai mérési módszer alapján

9.3. ábra - Partvonalhossz mérés eredménye és az értékek logaritmusa

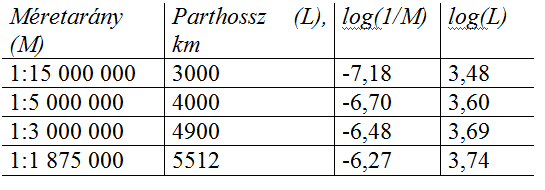
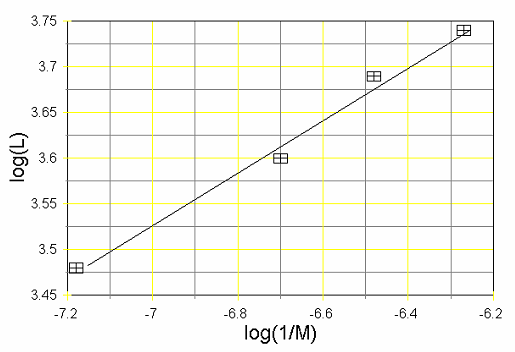
Ábrázoljuk a méretarány és a partvonal hosszának logaritmusait egy ún. log/log diagramon. A log/log ábrázolás megmutatja, hogyan változik a partvonal hossza (log(L)) a méretarány (log(M)) függvényében. A 9.3. ábra utolsó két oszlopának adatait grafikusan ábrázolva a 9.4. ábra mutatja.

9.4. ábra - Partvonalhossz mérés eredményének log/log diagramja

Keressük meg a kapott ponthalmazra a legjobban illeszkedő egyenest a legkisebb négyzetek módszerével.

A legjobban illeszkedő egyenest a következő alakban keressük:

Innen:

Azaz L parthosszúság egyenes arányos a méretarány d-edik hatványával.

Figyeljük és jegyezzük meg a d (meredekség) és a b (függőleges tengelymetszet) értékeit a számítással vizsgált esetben:

d = 0,29,

b = 5,6.

Például M=1:1 méretarányban (terepen) mérve, L = 10^5,6 = 398 000 km!

Ha M=1/n helyettesítést elvégezzük, akkor kapjuk, hogy

vagyis ha n tart 0-hoz ("végtelen nagy méretarányban ábrázolunk"), akkor

Azt kaptuk, hogy ha a méretarányt minden határon túl növeljük, akkor a partvonal hossza végtelen!