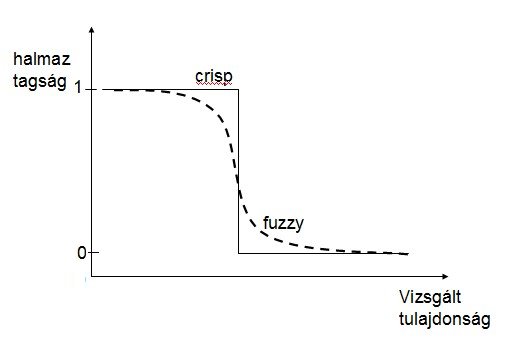
A fuzzy halmazok eredete Lofti A. Zadeh 1965-ben írt tanulmányához köthető, amiben azt állította, hogy bizonyos jelenségeket, eseményeket ne diszkrét formában kezeljünk konkrét határokkal (crisp), hanem ún. lágy határú (fuzzy) halmazokként (8.1. ábra).

8.1. ábra - A crisp és fuzzy halmazok

A módszer magyarázatához vissza kell nyúlni a Boole-algebrához, mely csak azt a helyzetet képes kezelni, hogy valamely elem (ez származhat az élet bármely területéről, későbbi példáinkban a raszteres geoinformatikából, ahol az elem egy pixel) vagy tagja egy halmaznak vagy nem. A határok merevek, ami bizonyos helyzetekben teljesen (átment valaki egy vizsgán vagy nem; van jogosítványa vagy nincs; ott van valami vagy nincs stb.), más esetekben – ha kritikákkal is –, de még elfogadható (hány ember szállhat be biztonságosan egy liftbe; mennyi lehet a megengedett sebesség személygépkocsival lakott területen belül; mennyi az egészségügyi határérték a szennyezőanyagokra). Sokszor azonban – amellett, hogy merev határokat alkalmazunk – a fuzzy lágy határai kézenfekvőbbek lennének.

Először nézzük meg a merev rendszerekre hozott példák kritikáját. Egy liftben elfogadható, ha megadunk egy maximális befogadóképességet, mert az emberek nem fogják ott helyben kiszámítani, hogy mekkora tömegűek együtt és a maximált létszámmal biztosítjuk a biztonságos terhelést. Annak az esélye, hogy csupa olyan ember száll be a liftbe, akik tömege a kalkulált átlagérték felett van, viszonylag kicsi és a rendszert úgy tervezték, hogy még ez se okozzon problémát. A települések belterületén több esetben a gyalogosok biztonsága szempontjából sok a megengedett 50 és 30 km/h, azonban a közlekedők biztonsága mellett biztosítani kell a dinamikus előrehaladást is. Ez esetben is egy olyan felső határt kell betartani, ami bár átléphető (annak tudatában, hogy ezért büntetés is járhat), de a tapasztalat alapján kevesebb baleset történik, mint a korábbiakban (kb. az 1990-es évekig érvényben lévő) megengedett 60 km/h óra mellett. A környezetvédelemben gyakran alkalmazott egészségügyi határértékeket is úgy határozták meg, hogy garantálja azt, hogy betartva őket az emberek környezeti eredetű terhelése is minimális lesz. Ha valahol, vagy valamiben mégis több a koncentráció, mint a megengedett érték, sokszor akkor sem történik baj (kivételek persze vannak, gondoljunk az évről évre ismétlődő CO-mérgezésekre), de kell egy betartandó határ, mely irányadó és számon kérhető. Vagyis (majdnem) minden merev halmazzal szemben is meg tudunk fogalmazni valamilyen kritikát, ugyanakkor fontos az egyszerűség is a betartás, betarthatóság és ellenőrizhetőség érdekében.

Ezekből a példákból is láttuk, hogy újra és újra felmerül a kérdés, hogy akkor pontosan mi is számít egy halmaz határának. Egy, a matematikai statisztikából vett példával nézzük meg, hogy milyen következményei lehetnek annak, ha a határokat mereven kezeljük. Fischer nevéhez fűződik a sok tudományterületen alkalmazott 95%-os valószínűség, ami azt jelenti, hogy 100 esetből 95-ször igaz az állításunk. De mi a helyzet a 94%-os valószínűséggel? Ez klasszikus értelemben már „nem szignifikáns”, azaz a nullhipotézist megtartjuk. Helyesen tesszük mindezt? Ha mereven kezeljük a szignifikancia határát, akkor igen. Sokáig tartotta magát ez a nézet, mára azonban nem véletlenül írjuk ki a szignifikancia pontos szintjét a p<0,05 vagy p>0,05 helyett, amik mögött nem látjuk a valódi értékeket. Vagyis, ha egy konkrét számhoz mérjük az elfogás/elutasítás határát, akkor azt kockáztatjuk, hogy elutasítunk, vagy megtartunk egy helyes hipotézist (vö. első és másodfajú hiba), ahol a 95% alatti valószínűséget akár kis elemszámú adatsorok, vagy hibás mérések is okozhatják. Ha viszont rugalmasan kezeljük és elfogadjuk, hogy 90%-tól már van bizonyíték a nullhipotézis elfogadása ellen, akkor közelebb járunk a valósághoz.

A fuzzy halmazoknak éppen az a lényege, hogy nem merev határokat húzunk, hanem megadjuk a halmazbeli tagság alsó és felső határát. Képzeljük el, hogy létezik egy klub (azaz egy halmaz), amibe csak magas embereket fogadnak be tagként (a halmaz elemei). Ha merev határt alkalmaznak és azt önkényesen pl. 190 cm-nél húzzák meg, akkor a 189 cm magas emberek kimaradnak a klubból (Kóczy és Tikk, 2001). A fuzzy halmazok alkalmazásával ezt úgy lehet elfogadhatóbbá tenni, hogy meghúzunk egy olyan alsó határt, melytől már be lehet lépni a klubba, de nem adunk meg hozzá minden jogosultságot: azaz pl. 180 cm-től tag lehet mindenki, de magasabb tagdíjat kell fizetni, vagy a gyűléseken önálló indítványt nem lehet előterjeszteni. 200 cm-től (mint a teljes tagság határától) viszont már nem kell tagdíjat fizetni és a gyűléseken ingyenes számukra a vacsora.

Ezekből az egyszerű példákból kiindulva számtalan tudományterület alkalmazza és sok olyan helyen találkozhatunk vele a gyakorlati életben is, ahol nem is sejtjük: képfeldolgozási eljárásokban, háztartási gépekben, szennyvízelvezetésben, a mozdonyok lassításában, űrkutatásban, haditechnikában (Kóczy és Tikk, 2001). A továbbiakban a környezet- és tájkutatásban alkalmazható lehetőségeket mutatjuk be. Célunk az, hogy a hallgatók tisztában legyenek a fogalmi háttérrel és alkalmazni tudják ezeket az ismereteket saját szakterületükön belül.