A földtudományokban igen fontos, hogy megfelelően tudjuk kezelni a mérési bizonytalanságokat. El kell fogadnunk azt a tényt, hogy az eredményeket, amiket a műszereink mutatnak, számos külső körülmény befolyásolja. Először is minden műszernek van alsó és felső méréshatára, mely alatt és felett az eredmények nem megbízhatók. Másodszor, a mérés során is lehet olyan feltétel, aminek a pontos végeredményhez teljesülnie kell és sokszor ezeket nem tudjuk, hogy kontrollálták-e. Egy olyan egyszerű mérés, mint a pH meghatározása is magában rejti a hibák lehetőségét: a folyadékban, szuszpenzióban a H3O+-ionok aktivitásának a mérése a pH-mérők üveg- és gélelektródáinak alkalmazásával egy egyensúlyi folyamat eredményeként számszerűsíthető. Ha nem várjuk ki azt az időt, míg az elektród felületén kialakul a folyadékra jellemző egyensúlyi helyzet, rossz eredményt olvasunk le. A végén egy adattá válik egy táblázatban, amivel dolgozunk. Sosem tudjuk meg, hogy a végleges értéket olvasták le a laboratóriumban (amire akár 10 percet is várni kell), vagy egy közbülsőt (amit lehet, hogy fél perc után írt ki a műszer). Mindezeken túl, számos hibát lehet elkövetni magával a mintavétellel és a mérések minden szakaszában. Sok esetben nem is áll rendelkezésünkre olyan adat, amire valójában szükségünk lenne (pl. szivárgás modellezésekor több mélységből szivárgási tényező 3 irányban), így meg kell elégedni valamilyen kompromisszum jellegű megoldással. Ezekben az esetekben hasznos lehet a fuzzy megközelítés, számolva a mérési hiba varianciájával vagy a rendelkezésre álló adat hiányosságaiból következő problémákkal.
A fuzzy halmazok igen jól implementálhatók geoinformatikai környezetbe. A térbeli jelenségek esetében is számos olyan feladat merül fel, ahol a fuzzy modell alkalmazása jobbá teheti a kapott végeredményt.
Vegyük példaként a hidrogeológiai védőterületek kijelölését. A kijelölés alapja az elérési idő, mely az az időtartam, amely alatt egy adott pontból a vízrészecske eljut a vízkivételig. A belső védőövezetben a vízkivételi hely környezetében a 20 napos elérési időt kell alapul venni. Ha ez a távolság kisebb, mint 10 m, biztonsági okokból akkor is legalább 10 méteres távolságot kell megtartani. Ez akkor azt jelenti, hogy pl. 11 méteres távolságtól már bármilyen tevékenységet lehet végezni? Valójában nem, mert a belső védőövezet után következik a külső védőövezet (6 hónapos elérési idő, minimum 200 m), majd a hidrogeológiai védőövezetek következnek. Ebben a sorrendben – akár mint egy fuzzy modellben – egyre többféle tevékenységet engedélyez a szabályozás. Fuzzy megközelítéssel ezeket a távolságokat is be tudjuk állítani és akár finomíthatjuk is a távolság függvényében.
A következő példában nézzük meg, mindez hogy néz ki a gyakorlatban. Az IDRISI-ben beállítottuk a védőterületek határait a következő paraméterekre mind a hagyományos Boole-alapú, mind a fuzzy módszerhez (8.6. ábra).
Szigmoidális modell:
- maximális védelem (belső védőterület): 20 m;
- nem védett terület (hidrogeológiai védőzóna külső határa): 800 m.
Lineáris modell:
- maximális védelem (belső védőterület): 20 m;
- nem védett terület (hidrogeológiai védőzóna külső határa): 800 m.
J-shape modell: - maximális védelem (belső védőterület): 20 m;
- nem védett terület (hidrogeológiai védőzóna külső határa): 800 m.
Egyedileg beállított, a védőterületeken alapuló modell:
- belső védőterület: 20 m;
- külső védőterület: 200 m;
- hidrogeológiai védőzóna (A): 500 m;
- hidrogeológiai védőzóna (B): 700 m;
- hidrogeológiai védőzóna (C): 800 m.
Sokszor kerülünk olyan feladat elé, hogy több térképfedvény felhasználásával meg kell mondanunk azt a helyet, mely bizonyos előre definiált szempontok alapján a legoptimálisabb. A hagyományos (crisp) ÉS/VAGY műveletekkel közelítve a feladat megoldását csak azt tudjuk megállapítani, hogy hol van a szempontjaink szerinti optimális terület határa és nem lehet figyelembe venni a belső heterogenitását, textúráját, illetve a távolsággal való változó megfelelést a kritériumnak, vagy csökkenő/növekvő valószínűségeket.
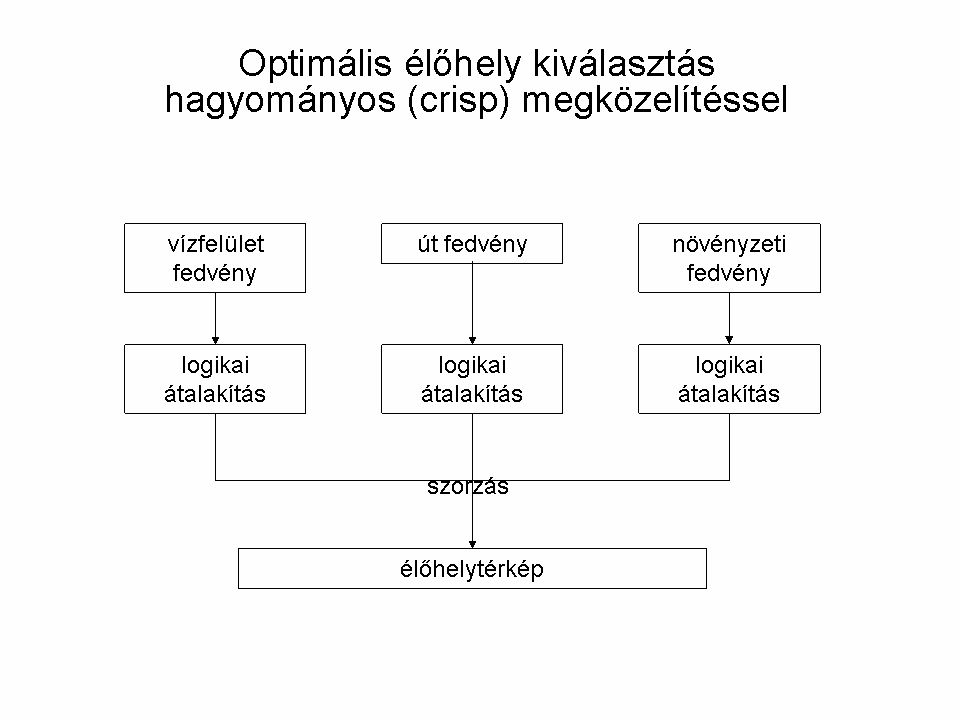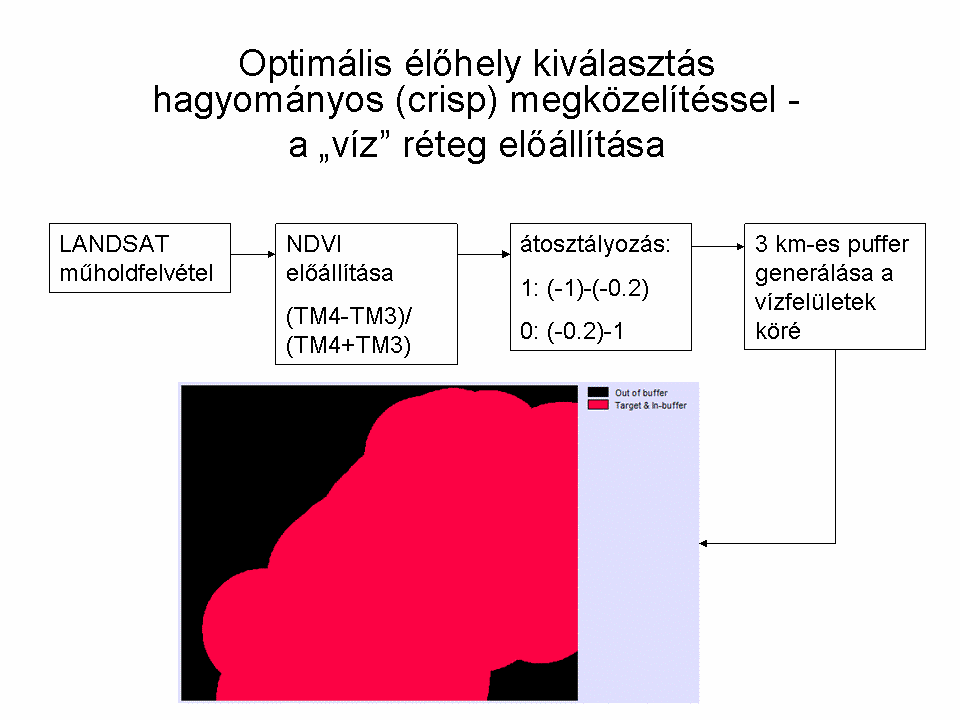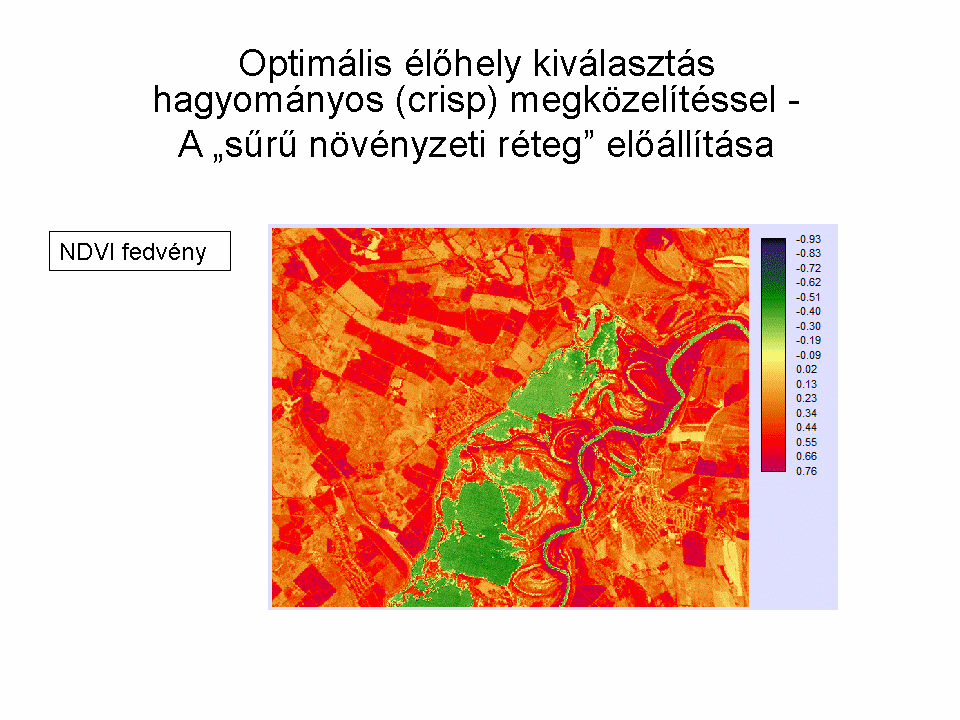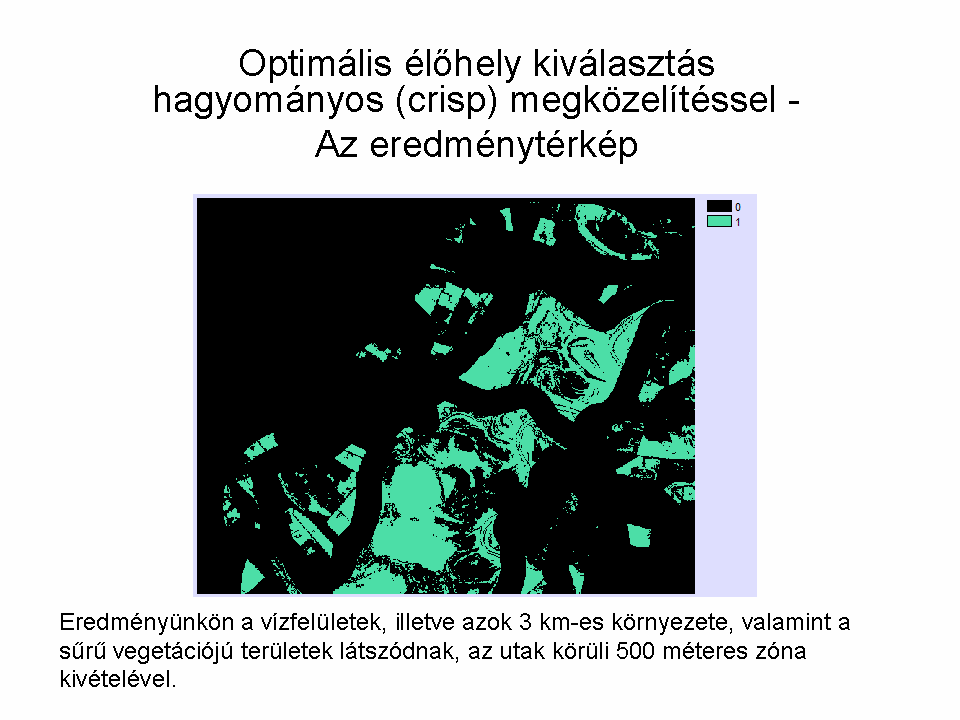
Példánkban tételezzük fel, hogy egy (elméleti) madárfaj erősen kötődik a vízhez, 3 km-nél ritkán távolodik el tőle, valamint a forgalmas utakat elkerüli kb. 500 m-es távolságban. Mindemellett kedveli a sűrű növényzetet. Keressük meg az optimális élőhelyét a fajnak. Mind a hagyományos, mind a fuzzy alapú megoldási lehetőségeket nézzük meg (8.7.-8.10. ábrák).
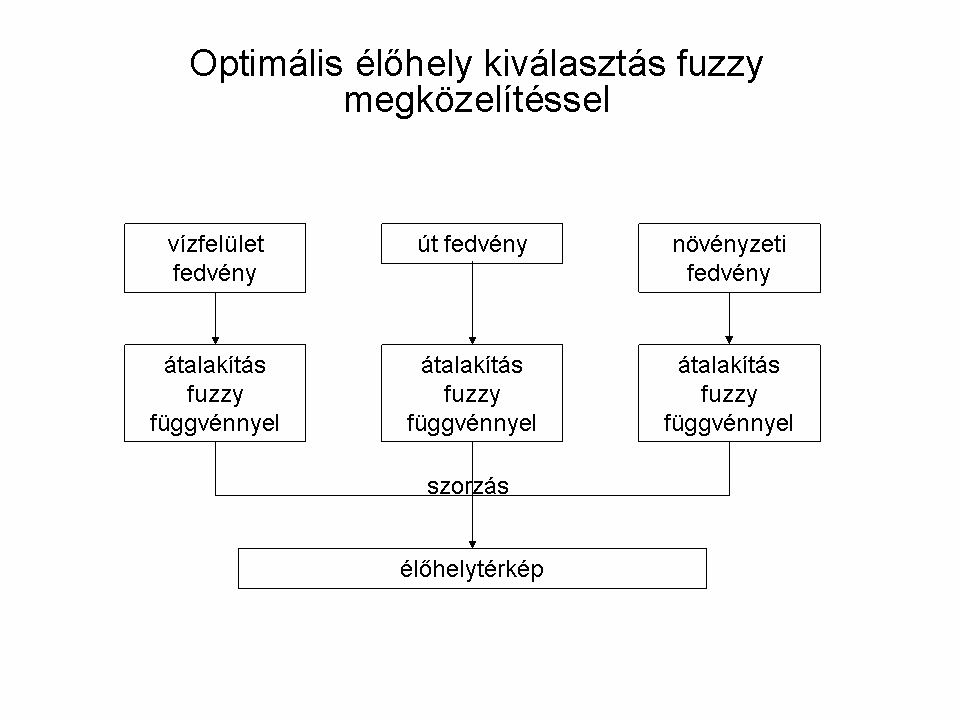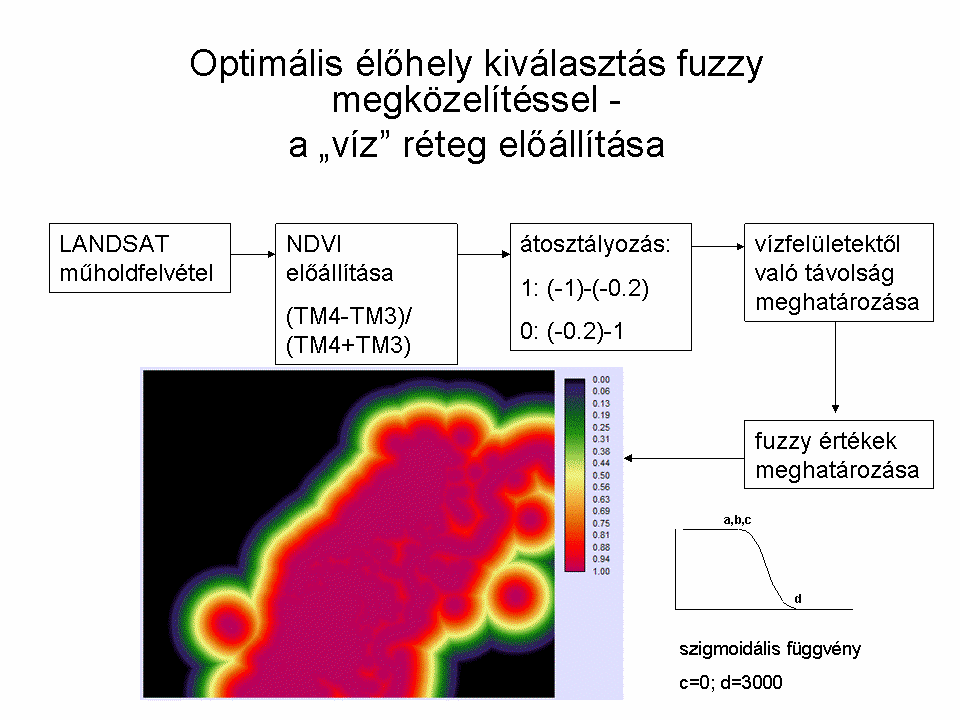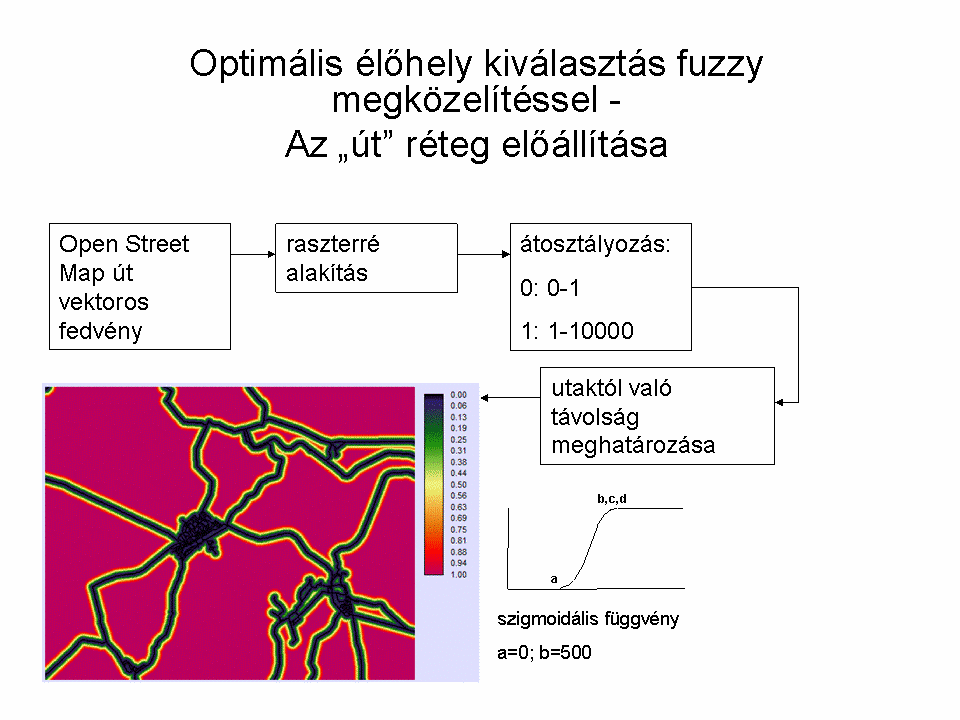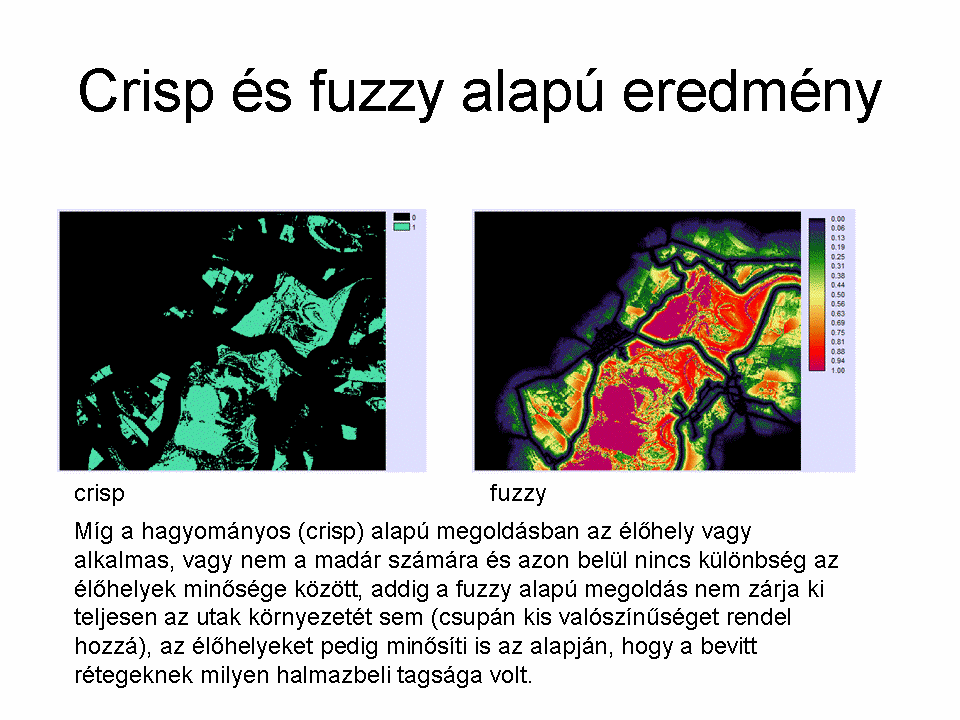
A megoldás során egy LANDSAT felvétel (mellékelve, LANDSAT Program, 2008) NDVI értékeiből átosztályozással megadjuk a vízfelületeket (-1 és -0.2 közötti értékek esetünkben jól visszaadják a vízfelületeket). Az OpenStreetMapről letöltött fedvény adja meg az utak rétegét. Ezekből előállítjuk a puffer zónákat a hagyományos megoldáshoz, illetve a távolság rétegeket a fuzzy halmazok bemenő adataként. Ezt követően a út-távolság fedvényre beállítjuk az 500 m-es távolságot. Mivel a vízfelületek is és a sűrű növényzet egyaránt fontos a szóban forgó madarak számára, csak egyedileg definiált fuzzy halmazzal tudjuk megadni a halmazbeli tagságot:
- (-1)- (-0,2) között 1, mivel ezek jórészben a vízfelületek (ezen a mintaterületen);
- (-0,2)-0 között 0,5 mivel itt még vizes foltok előfordulnak, a halmaztagságot is magasabb szinten tartjuk;
- 0-0,2 között 0,2 a gyér növényzet miatt; majd három lépésben növeljük a területek halmazbeli tagságának az értékét a teljes tagságig;
- 0,2-0,5 között 0,5;
- 0,5-0,7 között 0,8;
- 0,7 fölött 1.
A geoinformatika egyik fő alkalmazási területe a tájhasználat változásának vizsgálata. Ezek a vizsgálatok azonban több problémát is felvetnek: (1) mennyire pontos a tájfolt határa és (2) mennyire pontos a vetületbe illesztése a vizsgált térképeknek.
Különböző időpontok között lezajlott változásokat rendszerint kereszttabulációval (Kappa Index) vizsgáljuk (lásd 7. fejezet). Ez azonban feltételezi azt, hogy a folthatárok minden esetben hasonló módszerrel kerültek kijelölésre és azt is, hogy nem találunk egymás felett elcsúszó poligonokat amiatt, hogy az (orto)rektifikáció hibája túl nagy volt és az azonos helyeket jelölő pixelek nem fedik egymást (8.11. ábra).
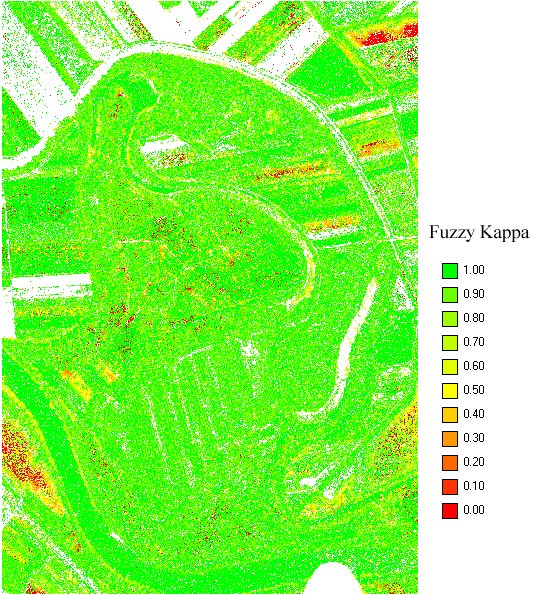
Sajnos ezek a feltételek rendszerint soha nem teljesülhetnek, mivel a régi térképek, vagy légifotók hiba nélkül nem rektifikálhatók (mivel sok esetben nehéz megfelelő illesztő pontokat találni), így az összehasonlítások eredménye sem lesz mentes a hibáktól. Ezeknek a hibáknak a csökkentésében, a valósághoz közelebbi eredmények elérésében segít ez esetben is a fuzzy alapú megközelítés: ha elmossuk a foltok határait és nem éles vonalakként kezeljük őket, a fentebb említett hibák is csökkenni fognak. A fuzzy alapon definiált átmeneti sáv szélességétől függően akár teljesen megszüntethetők ezek a hibák, azonban ennek a kisebb foltok is áldozatául eshetnek (azaz pl. kis erdei tisztások tűnhetnek el az átmeneti sávban). Jelenleg egy szoftver, Map Comparison Kit képes az ilyen jellegű összehasonlításra a Fuzzy Kappa mutatóval (Visser és Nijs, 2006).
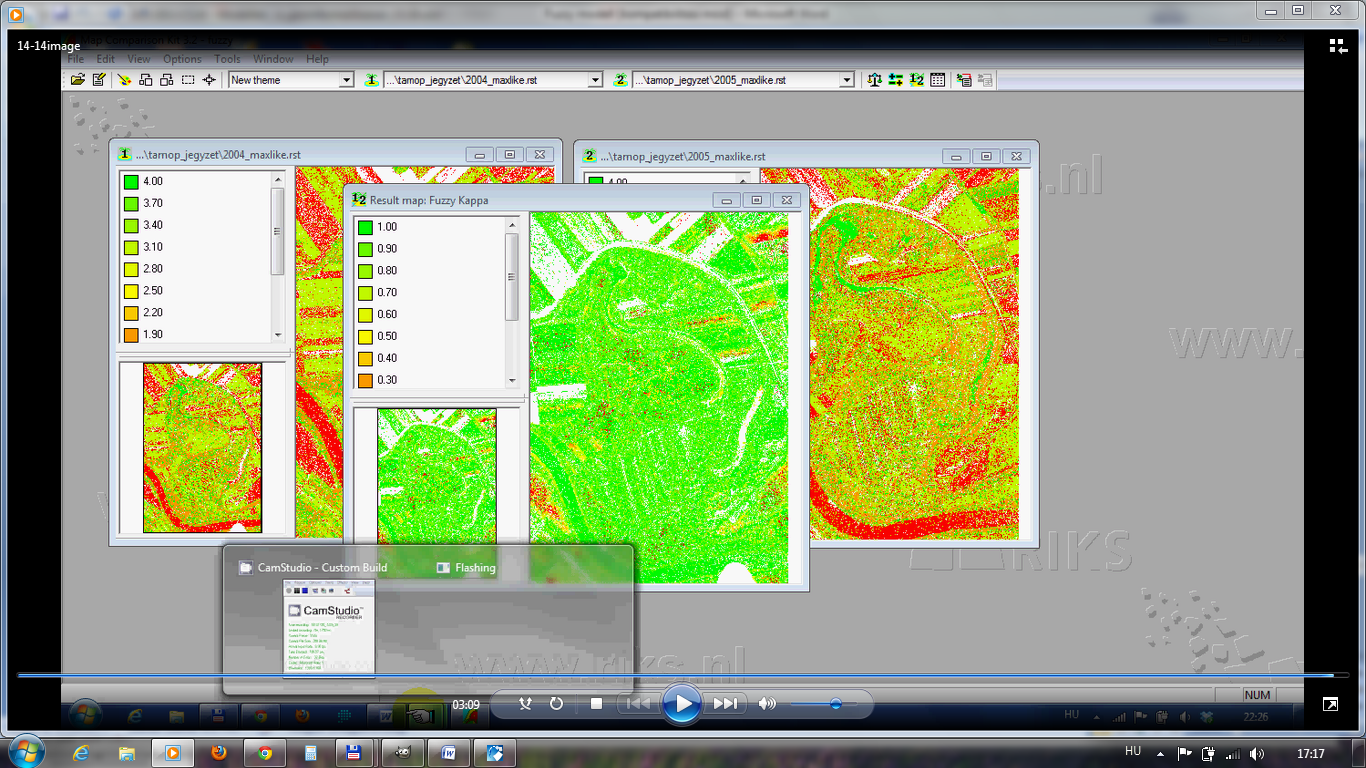
A Fuzzy Kappa a hagyományos Kappa Indexhez hasonlóan pixelenkénti összehasonlítás alapján számol, azonban a határt fuzzy alapon húzza meg a szomszédos kategóriák pixelei között (1: teljes egyezés, 0: teljes különbözőség).
Példánkban 2 légifotóról interpretált és szándékosan nem szűrt (azaz eléggé szórt pixeles) ellenőrzött osztályba sorolás eredményét vetjük össze (8.12 és 8.13. ábrák). A felvételeket 2 méteres felbontással vetettük össze, ahol a rektifikációs hiba miatt a pixelek nagy valószínűséggel nem voltak fedésben. Ezt bizonyítja a két felvétel Kappa Indexe (0,214), ami arra utal, hogy a két (ránézésre igen hasonló) térkép hasonlósága csak esetleges. Meg kell jegyeznünk azt is, hogy az is természetes, ha a két időpontban különbséget találunk: annak ellenére, hogy két egymást követő évről van szó, a felvételek készítési időpontja (adott éven belül) még ilyen kis időtávon belül is fontos lehet. A növényzet fejlettsége még, ha dátum szerint ugyanabban hónapban és napon volt is a felvételezés időpontja, akkor sem feltétlenül látjuk ugyanazt a képet, továbbá állapota függ a korábbi időszak csapadékmennyiségétől. Mindez hatással lehet a növények színére, ami automatikus osztályozásnál hibához vezethet (vizuális interpretációnál a probléma kezelhető). Jelen esetben azt szeretnénk megtudni, hogy milyen mértékű a változás a pixelek „elcsúszása” nélkül. A Fuzzy Kappa értékét pixelszám alapján kell állítani, melyet fel kell szorozni a 2 méteres felbontással, ha távolságokkal szeretnénk számolni. A keresési sugár – mely jelen esetben a határok közötti lágy átmenetért felel – alapbeállítása 4 pixel, a felezési távolság 2 pixel. Ezekkel a beállításokkal hasonlóan rossz eredményt kapunk a hagyományos Kappa Indexhez (0,255). Vagyis a vetületbe illesztés hibája több, mint 8 méter. 10 pixeles keresési sugárral és 2 pixeles felezési távolsággal a Fuzzy Kappa 0,203, azaz ezekkel a beállításokkal rosszabb lett az eredmény. 5 méteres felezési távolsággal azonban már 0,600 a Fuzzy Kappa. 20 pixeles keresési távolsággal és 10 méteres felezési távolsággal viszont már 0,852. Amennyiben 40 méteres a keresési sugár 20 méteres felezési távolsággal, még elképzelhető, akkor az eredmény is megfelelő (8.14.-8.16. ábrák).