Minden hagyományos Boole logikát követő megközelítés 1-et rendel azokhoz az elemekhez, melyek a halmaz tagjai, 0-át pedig a kívül eső elemekhez. A fuzzy halmazok esetében ez egy 0 és 1 intervallumba eső számérték, mely arányos a halmazbeli tagság mértékével (0: nem tagja a halmaznak; 1: teljes értékű tagja a halmaznak; a kis érték kismértékű halmazhoz tartozást jelez, a nagy érték nagymértékűt). Az átmenet fokozatos és az érték az ún. tagsági függvénnyel írható le, az általa definiált halmaz pedig a fuzzy halmaz (Kóczy és Tikk, 2001).
A függvények segítségével többféleképpen tudjuk definiálni a halmazok elemeihez tartozó értékeket. A főbb típusokat, melyek a legtöbb geoinformatikai szoftverben (pl. IDRISI, TAS, Whitebox GAT, SAGA GIS) is elérhetők, a következőkben ezek közül az IDRISI szoftver fuzzy-modulját ismertetjük (Eastman, 2012 nyomán). Rendszerint 2-4 értékkel kell megadnunk az egyes függvények alakját (lásd 8.2 – 8.5. ábrák):
-a: a halmazhoz tartozás kezdeti értéke (nagyobb, mint nulla),
-b: a halmaztagság értéke eléri az 1-et,
-c: a halmaztagság értéke 1 alá csökken,
-d: a halmazhoz tartozás megszűnik, értéke eléri az 1-et.
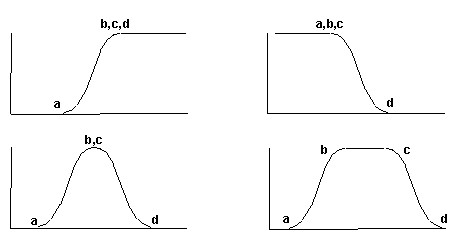
Ezek segítségével meg tudunk adni monoton növekvő, monoton csökkenő és szimmetrikus lefutású görbéket. Monoton növekvő görbénél a b-c-d értékek megegyeznek, ugyanígy a monoton csökkenő görbénél az a-b-c értékek ugyanazok. Mind a 4 érték megadása akkor szükséges, ha a halmazbeli tagságnak nemcsak egy irányban van határa, azaz adott elem veszíthet az értékéből, vagy el is veszítheti a tagságát meghaladva a határértéket (vagy a határérték alá csökkenve).
A leggyakrabban alkalmazott függvények a következők. Szigmoidális. A halmazhoz tartozás mértékét koszinusz függvénnyel írjuk le. A függvény által meghatározott görbe a klasszikus összetett lejtőkhöz hasonlít, melyek alsó része konkáv, felső része konvex és a kettő között félúton található az inflexiós pont (2. ábra). Gyakran alkalmazott függvénytípus.
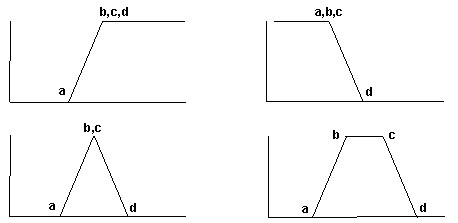
Lineáris. A függvénnyel lineáris szakaszokat definiálunk. Gyakran alkalmazzák egyszerűsége és az eredmények nyomon követhetősége miatt (3. ábra).
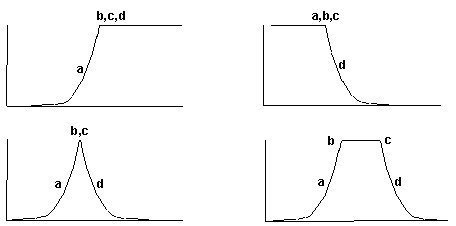
J-shape. A függvény lefutása valóban J-alakú, konkáv. Fontos tulajdonsága, hogy csak megközelíti a nullát, de nem éri el csak a végtelenben. Ez esetben az „a” és „d” pont nem a nulla értéket adja meg, hanem az inflexiós pontot, melynek értéke 0,5 (4. ábra). Ezen tulajdonságai miatt a földtudományokban kevésbé használják.
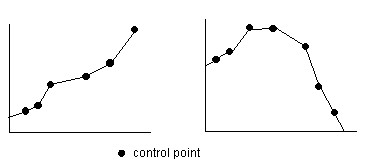
Felhasználó által beállított. A korábbi lehetőségektől eltérően, jóval több pontban is megadhatunk töréspontokat (egyenes szakaszokat definiálva), ami még inkább illeszkedhet az igényeinkhez és akár egy sokszoros feltételrendszernek (14-5. ábra).