A fejezet céljai: a fejezetben a rövid periódusú szénciklus avar-talaj részrendszerének modellegyenleteit írjuk fel, majd a tárolóegyenletek egyenletrendszerének két megoldását – egy algebrait és és egy numerikusat – adjuk meg. Betekintést kapunk a numerikus szimulációs programokban alkalmazott közelítő számítási módszerekbe.

Szükséges ismeretek, fogalmak: szénciklus, transzport ráta, mátrix műveletek, differencia egyenlet, Newton-féle hűlési törvény

2.1. Kompartment (kamra) modellek

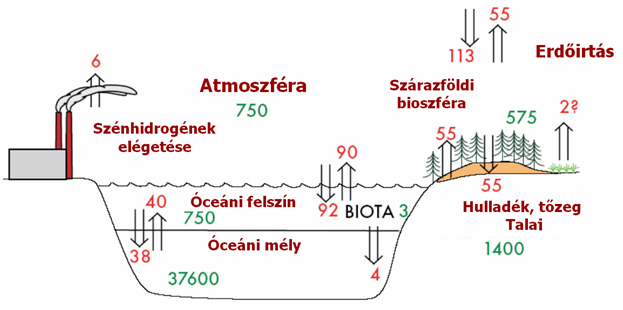
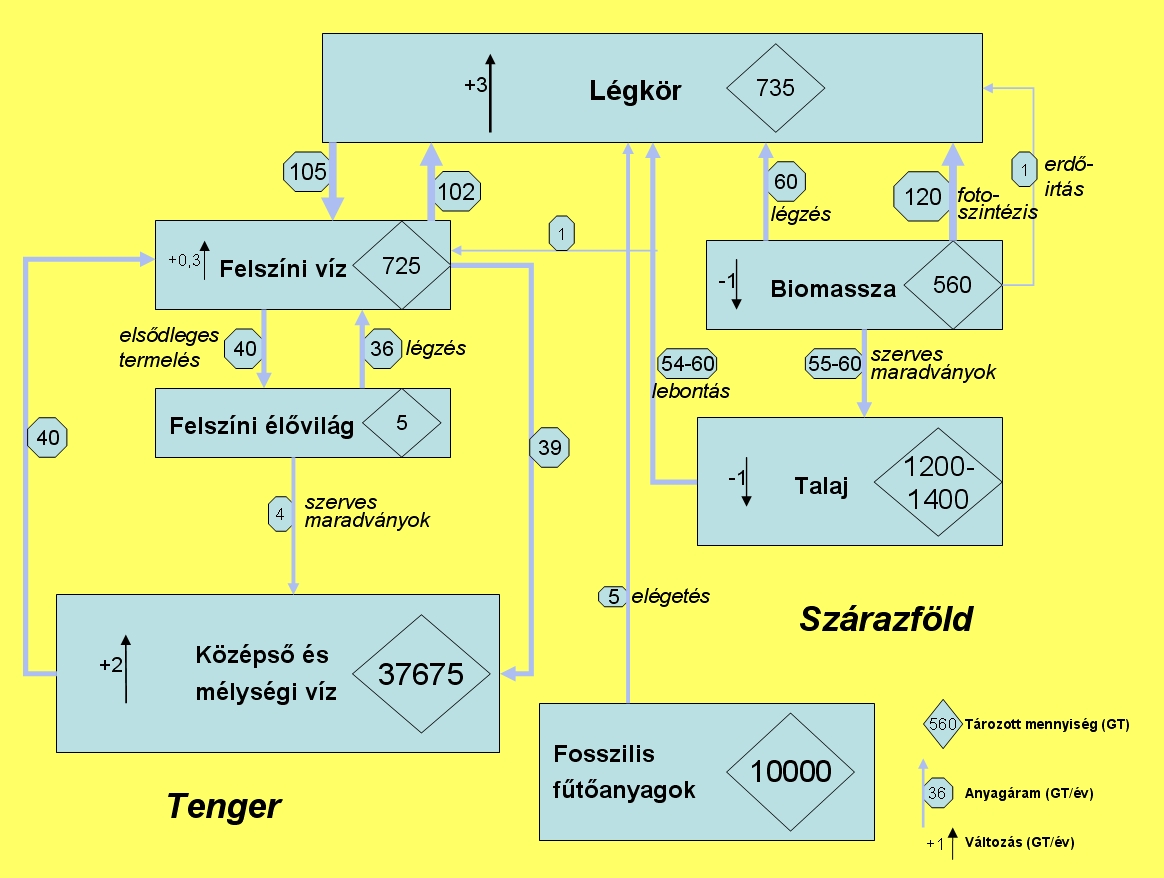
A különböző ásványi anyagok mozgásai, ciklusai az ökoszisztémákban jól tanulmányozhatóak az ún. kamra (kompartment) modellezési módszerrel. A folyamatok, legyen az globális pl. szénciklus (2.1. ábra), vagy lokális, pl. vízerózió egy kisvízgyűjtőn, megjeleníthetőek tárolókamrák, vagy rezervoárok halmazaként, amelyek között a kapcsolatot a be- és kiáramló anyagok mozgása jelenti (2.2. ábra, animáció.

2.1. ábra - Rövid periódusú globális szénciklus modell. Zöld értékek: tárolókban a tárolt, becsült szénmennyiség (GT); piros értékek: éves szénforgalom a tárolók között (GT/év)

2.2. ábra - Rövid periódusú szénciklus modell transzportfolyamatai, a tárolt és szállított szénmennyiségek (Kerényi, 1995 alapján)