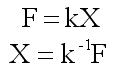A legegyszerűbb geokémiai ciklusok csak néhány tárolót tartalmaznak. Az alábbi példában az egyszerűség és a könnyebb megértés kedvéért csak két tárolókamrát – hulladék (avar) és talaj – veszünk figyelembe (2.3. ábra).
Jelölések: 1 : avar tároló; 2 : talaj tároló; x1 : széntartalom 1-ben; x2 : széntartalom 2-ben; t : idő; Δt : időlépcső; x1(t) : széntartalom 1-ben t időpontban; F12 : anyagáramlás adott idő alatt (= Fluxus) – két tároló között; 0 : környezet; F10 : anyagáramlás adott idő alatt az avar (1) tárolóból a környezetbe (0); F02 : anyagáramlás adott idő alatt a környezetből (0) a talaj (2) tárolóba
A tárolók széntaralmának változását a bejövő és a kimenő szénmennyiségek összege határozza meg. Δt idő alatt x1 és x2 tárolókban a széntartalom-változást felírhatjuk:
Másrészt igaz, hogy:
A jobb oldalakat egyenlővé téve és átrendezve kapjuk:
Ezek az egyenletek fejezik ki a kalibrálatlan modell alapállapotát.
A levelek, ágak és a gyökerek pusztulásából származó F01 és F02 szén inputokat tekinthetjük állandó értéknek. Az F10, F20 és F12 értékeket a modell kalibrálásával kapjuk meg.
Az outputokat lineáris transzport összefüggés adja meg, mely szerint a tárolók közötti anyagáramlás a „donor” kamrákban tárolt széntartalom valamely függvénye, általánosan
ahol kij a transzport rátája (üteme). További elnevezései: transzfer együttható, ráta állandó, körforgási ráta.
Példa: dinamikus egyensúlyban tárolt mennyiség 1000 kg/ha, output: 10 kg/ha/év, akkor k10 = 10/1000 = 0,01 = 1% .
A kij transzport ráta reciproka a körforgási idő, vagy a geológiában tartózkodási idő.
A modellre alkalmazva a lineáris transzporttörvényt:
A modell egyenletrendszerének megoldásával két kérdésre kaphatunk választ:
a.) hány év alatt, és
b.) milyen szinten áll be az egyensúlyi állapot az egyes tározókban?
Alkalmazzuk először a megoldás mátrixos módszerét. Behelyettesítve a transzport-egyenletekbe kapjuk:
Ezzel megkaptuk a modell alapját képező szimultán differencia-egyenlet rendszert. A modell kalibrációja jelenti, tehát az F01, F02 inputok és a k10 , k20, k12 körforgási ráták meghatározását a rendszer outputjából.
A rendszer egyensúlyi állapotba kerül, ha a tárolók széntartalma t idő eltelte után tovább már nem változik:
Azaz:
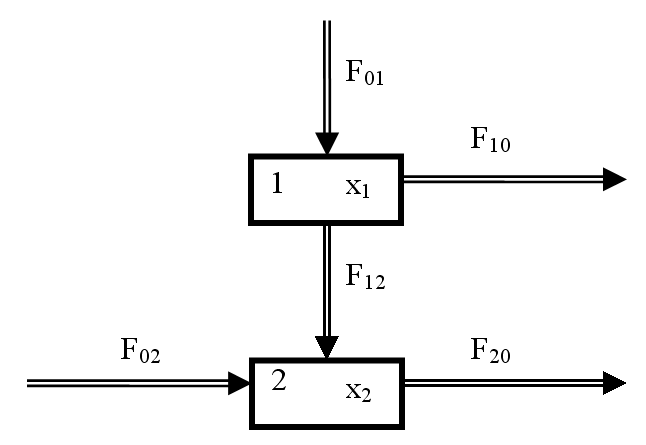
Átrendezve és mátrixokkal kifejezve, ahol a mátrixokat rendre jelöljük F, k, X, ekkor:
Kiszámítva k-1 inverz mátrixot és elvégezve a mátrixszorzást megkapjuk a b.) kérdésre a választ: egyensúlyi állapotban az állapotváltozók x1és x2 értékét. Ez a megoldás nem ad választ az a.) kérdésre!
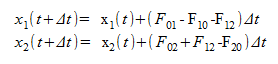
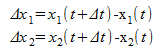
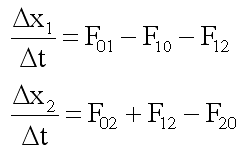
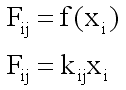
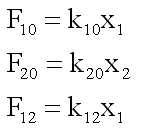
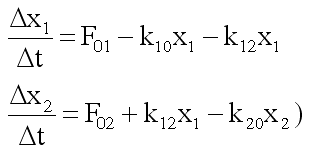
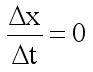

![left [ binom{F_{01}}{F_{02}} right ]=left [ matrix{k_{10}+k_{12} # 0 ## -k_{12} # k_{20}} right ] left [ binom{x_{1}}{x_{2}} right ]](Math/2-9eq.png)