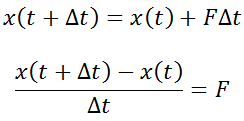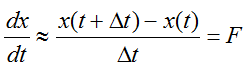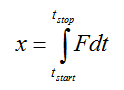A dinamikus rendszerek – melyek a legtöbb esetben folytonos állapotváltozással jellemezhetők (égitestek mozgása, hőmérsékletváltozás, stb.) - számítógépes modellszimulációja nem képes a tökéletesen egzakt megoldás előállítására, ehelyett diszkrét számítási eredmények sorozatával közelíti az elméleti (analitikus) megoldást.

A diszkrét rendszerekben a változók értékének számítása időlépcsőnként történik, pl. bankbetétünk után a kamatszámítás. A modell futtatásakor a program sztenderd numerikus számítási módszereket használ az egyenletrendszerek megoldásához.

Jelöljük:

x(t) : x tároló (állapotváltozó) értéke t időpontban

F = F(x(t)) : anyagáramlás (folyamatváltozó) értéke x tárolóhoz t időpontban

A tároló értékét a (t+Δt) időpontban megadja a következő véges differencia egyenlet:

Azaz F anyagáramlás értékét megadja az x tároló értékének Δt időtartam alatti megváltozása. Áttérve a differenciális formulára (Δt →0):

Ahonnan:

Ezt a kifejezést nevezik az elsőrendű differenciálegyenlet merőleges, vagy az Euler-integráljának. A valós folytonos rendszerekben tehát az állapotváltozó értékét a folyamatváltozó integrálásával határozhatjuk meg. A tárolók a modellekben a rendszerelemek állapotát, vagyis a változások eredőjét fejezik ki.

A folytonos változást numerikusan kifejezni nem lehetséges, ezért a változók értékét kis időlépésenként számítjuk. A szimuláció során minden időlépésben az állapotváltozók a rendszer pillanatnyi állapotának megfelelő értéket vesznek fel. Minden időtartamra a rendszer állapotváltozásának és az állapotváltozók differenciáinak számítása a feladat, amely integrálszámítási problémát jelent.

A véges differenciaegyenletek megoldása elméletileg egyszerű és a következő lépésekből áll:

1. Inicializálási fázis: az összes szükséges egyenlet sorbarendezése; az állapot- és folyamatváltozók kezdőértékeinek számítása.

2. Iterációs fázis: becslés az állapotváltozó értékének Δt időtartam alatti megváltozására. A tároló új értékének számítása a becslés alapján; a tárolók új értékének felhasználásával a folyamatváltozók új értékének számítása, majd a szimuláció léptetése Δt-vel. Az iteráció leállítása, ha t_start ≥ t_stop.

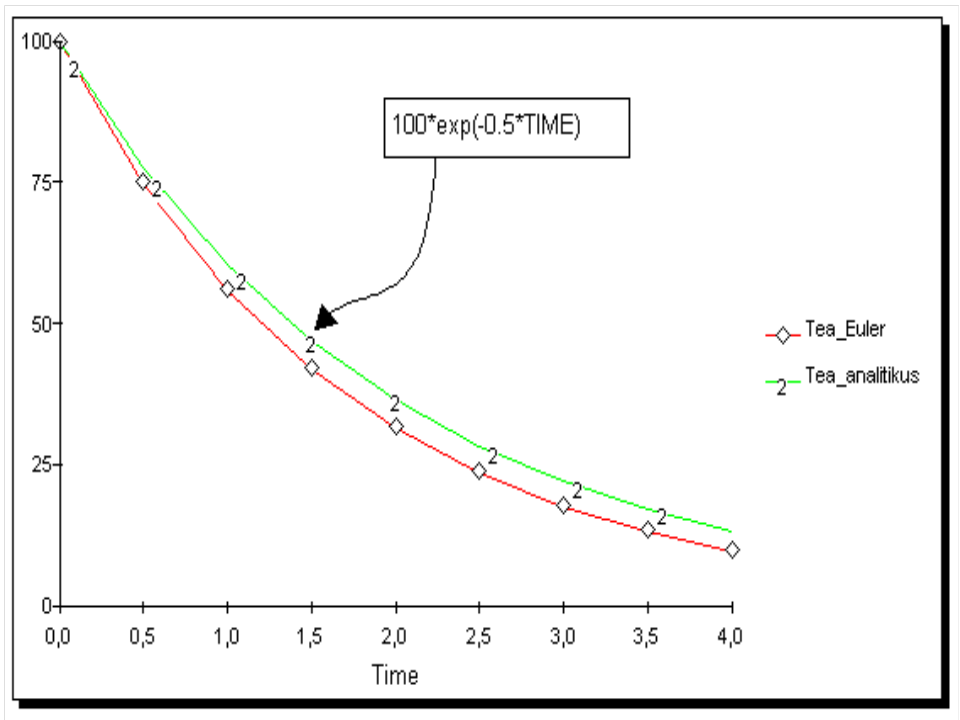
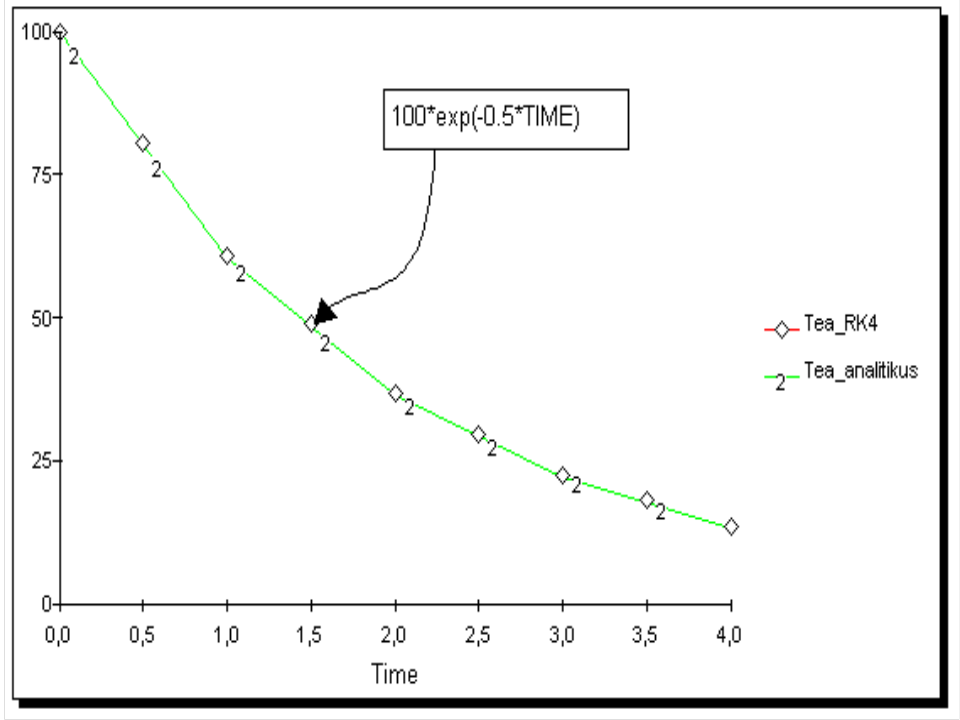
A legkritikusabb az iterációs fázis első lépése: hogyan becsülhető meg az állapotváltozó értékének Δt alatti megváltozása? A dinamikus rendszer-szimulációs programok erre a becslésre általában az ún. Euler- és Runge-Kutta (másod-, harmad-, negyedrendű) numerikus integrálási módszereket alkalmazzák. Egyszerű példa: Newton-féle hűlési törvény analitikus megoldása és numerikus számítása (animáció).

1.Euler-módszer

Összehasonlítva a grafikonokat láthatjuk, hogy a választott megoldási módszertől függően eltérés adódik az analitikus és a numerikus megoldás között (2.4-6. ábrák). Az analitikus és az Euler-módszerrel kapott görbe közötti eltérés az integrálási hiba, amely az Euler-módszernél a legnagyobb. A Δt időlépcső csökkentésével a hiba kisebb lesz, zérus közelében az Euler-módszer is az egzakt megoldást szolgáltatja. Ezzel viszont növekszik a számítási idő és a kerekítésnél elkövetett hiba. A Runge-Kutta módszerek nagyobb időlépcsőnél is pontosabb megoldást szolgáltatnak, viszont számítási igényük nagyobb az Euler-módszerénél.

2.4. ábra - Newton-féle hűlési törvény analitikus megoldása és numerikus számítása Euler-módszerrel

2. Másodrendű Runge-Kutta-módszer (javított Euler-módszer)

2.5. ábra - Newton-féle hűlési törvény analitikus megoldása és numerikus számítása másodrendű Runge-Kutta-módszerrel

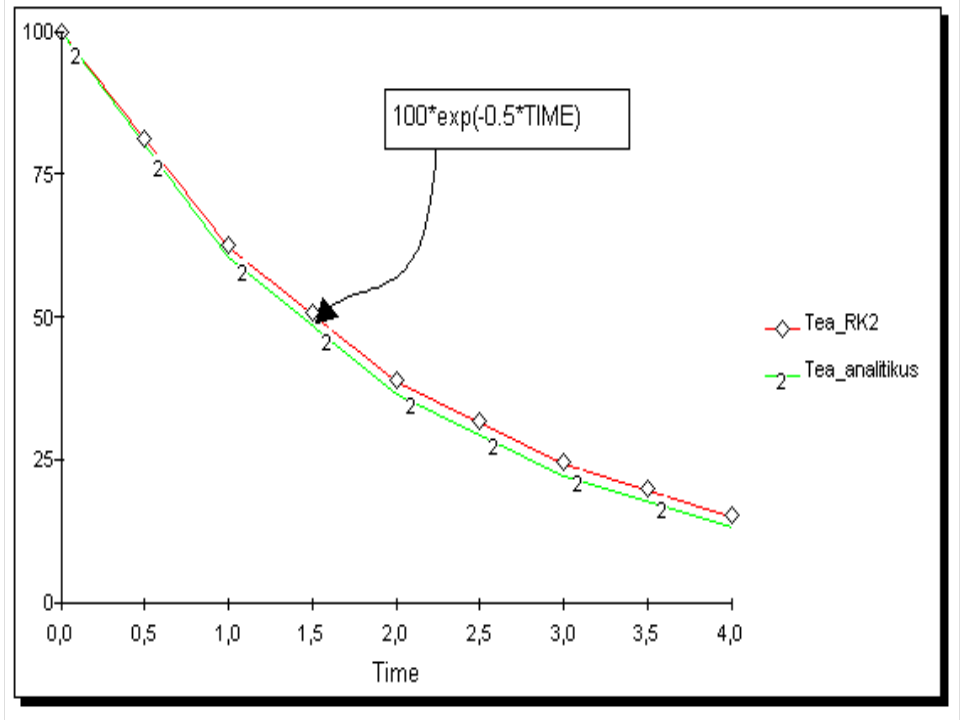3. Negyedrendű Runge-Kutta-módszer

2.6. ábra - Newton-féle hűlési törvény analitikus megoldása és numerikus számítása negyedrendű Runge-Kutta-módszerrel