A modelleket ma leghatékonyabban arra használják, hogy leírják, magyarázzák, ill. analizálják egy rendszer működését. Gyakran találkozunk velük a földrajz elméletében, ahol többnyire a megértést segítik és gyakorlatában, mint pl. a regionális tervezésben, a környezeti hatásértékelésben, vagy épp a döntéselőkészítésben, ahol e tevékenységek szerves részei (Mezősi, 1995).
Ugyanúgy modellnek tekinthető tehát a valóság grafikus, mint ahogy a matematikai képe is. Általában mondhatjuk, hogy a modell a valóság egy speciális vetülete, annak idealizált képe. Mondhatni minden tudományág elkészítheti a saját álláspontja szerinti definíciót, ha nem a természettudományos megközelítést tekintjük, akkor pl. a modell tartalmilag akár elmélet, törvény, vagy strukturalizált koncepció is lehet.
Ebből az igen szerteágazó kérdéskörből a lényeges számunkra az lehet , hogy a rendszereket a tartalmuktól elvonatkoztatva is lehet együttesen tanulmányozni (vö. von Bertalanffy-féle általános rendszerelmélet, azok hordoznak közös tulajdonságokat, amelyek nagyon sajátságosan jellemzőek egy-egy rendszerre továbbá a tapasztalt sajátságok, törvényszerűségek átvihetők.
A modell és a rendszer közötti kapcsolatot vizsgálva hasznos és szemléletes lehet Huggett (1980) által elkülönített rendszeranalízis fázisokra hivatkozni. Szerinte a rendszerek elemzésénél az alábbi 4 fázis épül egymásra:
-lexikai fázis, amikor próbáljuk megérteni a rendszer határait, tartalmát (változóit), az állandó változók értékeit;
-feltáró fázis, amikor a rendszer változói közti kapcsolatot próbáljuk definiálni, matematikailag, fizikailag, vagy verbálisan;
-modellező fázis, amikor egyrészt megkonstruáljuk a modellt, másrészt "futtattjuk" azt;
-elemző fázis, amelyben a modell érvényességét elemezzük.
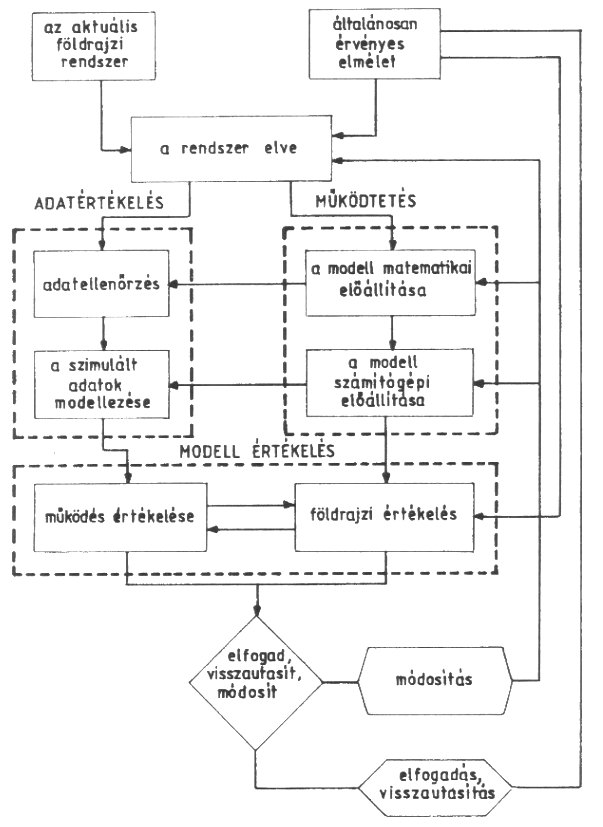
Ez persze nem jelenti azt, hogy modellel csak a 3. szinttől felfelé találkozhatnánk. Nagyon sok, a megértést könnyítő modell található pl. a lexikai fázishoz kapcsolhatóan (a tankönyvekben számos ilyen sémát találunk, s megállapodás kérdése, hogy ezeket minek nevezzük). Gyakori a feltáró fázis kimaradása is egyszerűen azért, mert a tényezők nehezen kvantifikálhatók. A modellezésnek hasonlóan felállítható egy releváns sorrendje (1.2.ábra):
-a modellalkotás, amely felhasználja a modell paramétereit és a köztük lévő kapcsolatot figyelembe véve az absztrakció, általánosítás és egyszerűsítés szabályait;
-a modell alkalmazása, amelynek célja pl. új információ, ismeret létrehozása, beleértve pl. a szimuláció nyújtotta lehetőségeket is;
-a modell értékelése (a modellezés kommunikációs része), amely a modell érvényességét az előállított eredmények figyelembe vételével elemzi, különböző szcenáriókat és alternatívákat vizsgál.
Ezek alapján sejthetők talán azok az előnyök, amelyek a modellek földrajzban történő használata mellett szólnak. Ilyen lehet többek között, hogy a szakmai kommunikáció egyik legkönnyebb módja, benne információk, elméletek, vélemények koncentráltan jelennek meg. Alkalmazásukkal különböző típusú problémák vethetők össze, s törvényszerűségek, szabályszerűségek adaptálhatók.
A modellek alkalmazásának célja, funkciói
A modellek alkalmazásakor alapvetően két nagy célcsoportot szoktak emlegetni. Az egyikbe a gyakorlatban (pl. a tervezésben, előrejelzésben, hatásértékelésben) használatos modellek tartoznak, amelyekkel valamit kiszámolunk, prognosztizálunk, értékelünk stb. A másikba - eléggé pejoratív használattal - a megértést célzó modellek kerülnek. Ez az igen gyakori csoportosítás azért sántít, mert az ún. gyakorlati, tervezési célú modellek is természetesen szolgálják a rendszer működésének megértését, másrészt a megértési célú modellek olykor nem tudnak végighaladni a rendszerépítés, modellalkotás fázisain a rendkívül nehézkes kvantifikáció miatt.
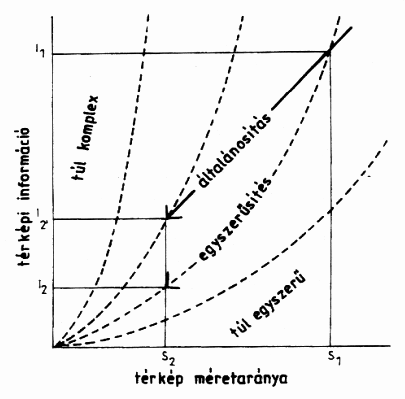
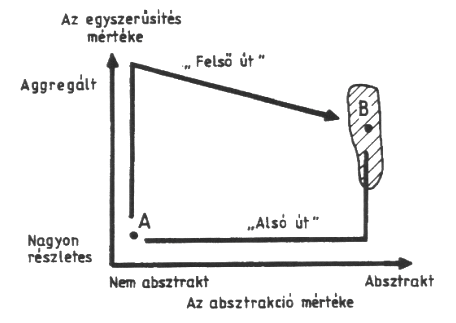
Valószínűleg a legbonyolultabb kérdések egyike a modellekkel kapcsolatban az egyszerűsítés, általánosítás (idealizálás) viszonya, ill. ezekkel szoros kölcsönhatásban a méretarány szerepe. Az minden modellépítéssel foglalkozó könyvben olvasható, hogy a modell alkalmazásának sikere nagyban függ az absztrakciótól. Arra nézve azonban már nagyon kevés információval rendelkezünk hogyan oldjuk meg az egyszerűsítést. Ami az egyszerűsítés és az általánosítás viszonyát illeti, arról a 1.3. sz. ábra térképészeti példája segít eligazodni. Mind az egyszerűsítés mind az általánosítás információvesztéssel jár. Ha lecsökkentem a méretarányt pl. 1:10 000-ről 1:100 000-re hirtelen túldúsul az információ, ellenkező esetben meg kiürül a térkép. Ilyenkor az a megoldás kínálkozik, hogy S1-ről S2-re való átmenetkor a pontsorral jelzett sávban maradunk az általánosítással, aggregált egységekkel a I2 helyett az I2’ javasolt (Mezősi, 1995). A modellezés, ill. a (dinamikus) szimuláció gyakorlatában általában azt az utat javasolják (POWERSIM, 1993), hogy először végezzük el az egyszerűsítést majd utána az általánosítást (az un. "felső út"), aki mégis az alsót választja, "adjon fel minden reményt" lásd (1.4. ábra).
A modellek jellemzőit Chorley, R.J. - Haggett, P. (1967) az alábbiakban foglalja össze:
-approximatív, azaz elég egyszerűnek kell lennie, a használatot, a megérthetőséget figyelembe kell venni, de ez nem járhat a komplexitás elvesztésével;
-szuggesztív, azaz le kell határolni mi a modell érvényességi köre, mi a viszonya a teljes modellhez (a földrajzban a méretarányok miatt ez igen fontos), mennyire képes a predikcióra stb.;
-szelektív, azaz információszűkítés árán - bizonyos esetekben a tényezőket eliminálva – csak "lényeges" paramétereket vesz tekintetbe;
-szerkezeties, azaz mind a rendszer taxonometrikus, mind viszonystruktúráját hordozza
-a modell különbözik a valós világtól, csak az analógia jelleg van meg;
-és valószínűleg a legvitatottabb jellemző az, hogy a modelleknek alkalmazhatóknak kell lenniük.
A típusainak csoportosítását leginkább csak azért mutatjuk be, hogy kitűnjön milyen sokszínű a modellek világa. Chorley, R.(1967) pl. így csoportosította azokat:
1.Analógián alapuló rendszerek:
a) történeti analógia ("a jelen a múlt kulcsa" Lyell pl. a geológiában, vagy a tájfejlődésnél, denudációs kronológia);
b) térbeli analógia (ezt a kategóriát méltán kritizálták, mert pl. a korábbi globális felmelegedés Budiko 1987 elve csak nagyon korlátozottan vihető át a jövőre).
2. Fizikai modellek:
a) hardver modellek (ezeknél a modelleknél - főként természetes - anyagot használnak, de tágabb értelmezésben a természetes anyagokkal kapcsolatba hozható minden modell ide tartozhat pl. talajerózió modellezése);
b) matematikai modellek
-determinisztikus (pl. lineáris egyenletrendszerek, differenciál egyenletek használata)
-sztochasztikus (statisztikai eljárások).
3.Általános rendszerek (ezek többnyire elméleti modellek, és mint az előzőekben erre utaltunk, ezek egyúttal a részletesség, ill. a felbontás problémáját is jelzik)
a) szintetikus (fehér doboz minden kapcsolat és a folyamatok is ismertek, ezek többnyire ún. homomorf modellek, azaz csak néhány elemet tartalmaznak)
b) parciális (szürke doboz itt a tényezők kapcsolatait ki tudjuk matematikailag fejezni, de a folyamatokat nem tudjuk leírni)
c) fekete doboz modellek (csak a ki- és a bemeneti információk ismertek, ilyenek pl. az izomorf modellek, amelyek minden elemet tartalmaznak).