A vizsgálatok egy külön csoportját alkotják a tájmetriai indexek. Az indexek elméleti alapját McArthur és Wilson (1967) szigetbiogeográfiai megfigyelései adják. Az elmélet a szigetbiográfia elnevezést onnan kapta, hogy a szigetek fajdinamikájával kapcsolatos megfigyeléseket ültették át a szárazföldi folt-folyosó-mátrix megközelítésbe. A tájban nem lineáris elemként megjelenő környezetétől eltérő viszonylag homogén egységeket (felszínborítottsági kategóriákat, vagy részletesebb vizsgálatok alapján társulásokat) foltként; a foltok közötti fajok áramlását biztosító hosszan elnyúló (lineáris) egységeket folyosóként, a foltok beágyazó felületét (egyes esetekben legösszefüggőbb, vagy legelterjedtebb elemét) pedig mátrixként értelmezzük. Főbb megállapításaik a következők:
-a mátrix a tengerhez képest átjárhatóbb (a fajoknak nem kell repülni, vagy úszni tudniuk a foltok közötti távolságok áthidalásához);
-a nagy foltok fajgazdagsága nagyobb, mint a kisebb foltoké;
-a nagy foltokhoz (mint kontinenshez) közeli foltok fajgazdagsága nagyobb, mint a távolabbi foltoké (szigeteké), az előbbi nagyobb betelepedési rátája miatt;
-a foltok mérete és a fajok száma közötti az összefüggés csak egy bizonyos méretig lineáris, utána a fajnövekedés mérsékeltebb – a tájfoltokra vonatkoztatva ennek a megfigyelésnek a megfordítását kell alkalmazni: az élőhely-vesztés során létezik egy olyan kritikus foltméret, ami alatt a fajok kihalása felgyorsul (Forman, 1995; Kerényi, 2007).
A mérőszámok mára túlléptek azon, hogy csak az egyedi foltokra vonatkozó tulajdonságokat jellemezzék, de természetesen ezek továbbra is fontos részét képezik a tájanalízisnek. A tájmetriai indexeket 3 szinten definiálhatjuk: (1) a hagyományos folt szinten, (2) osztály szinten és (3) táji szinten. Folt szinten az indexek az egyes foltok területét, kerületét, terület/kerület arányát stb. adják meg. Az osztály szintű mutatók az ugyanabba a kategóriába tartozó foltok aggregált jellemzőit adják meg egyszerű, vagy súlyozott átlagként, vagy olyan tulajdonságaikat is figyelembe veszik, amikkel a térbeli elhelyezkedésükre (területi eloszlás, közelség, konnektivitás) tudunk következtetni. Táji szinten az indexeket a táj összes foltjának a tulajdonságai alapján számítjuk (Forman és Godron, 1995; McGarigal és Marks, 2002).
Az 1980-as évek során igen nagy mennyiségben fejlesztettek ki tájmetriai indexeket. Használatukat nagymértékben megkönnyítette a GIS szoftverek megjelenése és elterjedése, valamint az egyre olcsóbban és nem utolsó sorban könnyebben hozzáférhető légifotók és műholdfelvételek alkalmazása.
Az egyes indexek között nagy az átfedés, erősen korrelálnak egymással. Az átfedések kiszűrésére több próbálkozás is történt, melyek közül a legismertebbet, Riitter és munkaársai 1995-ben írt munkáját kell kiemelni, melyben 85 térképből számított 55 tájmetriai mutatót dolgoztak fel, melyek számát a szoros keresztkorrelációk és a normalitás feltételének megsértése miatt 26-ra csökkentette. A vizsgálat során a 26 metrikát 6 főkomponensben egyesítették: foltkompaktság; folttextúra; foltalak; attribútum osztályok száma és a nagy foltok kerület/terület fraktáldimenziója. Hozzá kell tenni azt is, hogy a szerzők maguk is kétségbe vonják az eredmények jelentőségét, mivel csak egyetlen vizsgálati helyszín azonosítását tették lehetővé (ami ráadásul egy kiugró értéket képviselt). Általánosan megfogalmazhatjuk, hogy nem tudjuk definiálni azoknak a mutatóknak a teljes körét, amik a tájanalízisben bárhol általánosan felhasználhatók, mert a mutatók fentebb említett korrelációja nem állandó, így a különböző statisztikai feldolgozások sem ugyanazt az eredményt adják.
A tájmetriai kutatások rendszerint a foltokat teszik a vizsgálatok tárgyává, mivel ezek geometriai tulajdonságai (terület, kerület, alak stb.), valamint relatív térbeli elhelyezkedése (pl. foltok közelsége, konnektivitás) geoinformatikai módszerekkel matematikailag egyszerűen számítható.
A tájmetriai feldolgozások során el kell fogadnunk néhány olyan korlátozó tényezőt az ökológiai-tájökológiai alaptételekkel kapcsolatban, ami miatt az eredmények interpretációja kissé eltérő. Az okok a számítástechnikai feldolgozás kötöttségéivel, pontosabban a módszerek egyes esetekben kevéssé kidolgozott jellegével magyarázhatók.
1.A feldolgozás során nem teszünk különbséget a lineáris és nem lineáris tájelemek között, minden környezetétől elütő egységet foltként értelmezünk.
2.A foltok rendszerint a mátrix-szal határosak, azonban sokszor a mátrix is foltokból áll, így a feldolgozás során foltként számolunk vele, mivel a mátrix és a folt között geometriai és topológiai értelemben nincs különbség (és az előző pontban megfogalmazottak miatt ide soroljuk a folyosókat is). Két dolgot tehetünk: (1) elfogadjuk ezt a tényt és a foltként értékeljük a mátrixot is; (2) a mátrixot kihagyjuk a számításból.
3.A szoftverek döntő hányadába nincs beépítve az antropogén gátak figyelembe vételének a lehetősége. A foltok közötti legrövidebb távolságok helyett több szoftverrel is van lehetőségünk „ökológiai” távolságokkal kalkulálni (azaz figyelembe venni a mátrix heterogenitását, illetve az ökológiai gátakat). A számításokat rendszerint legkisebb távolságokkal végezzük, ezért a fragmentációra, izoláltságra és konnektivitásra tett megállapítások jó része az antropogén eredetű ökológiai gátaktól mentes természeti tájra vonatkoznak. Így valójában, amikor a fragmentációról esik szó, a természeti tájak mozaikosságát kell alatta érteni. Az eredmények interpretálása során pedig ehhez kell tartani magunkat: ha a fogalmi hátteret tisztázzuk, akkor a felhasználó is tudni fogja, hogy a megállapítások művi elemekkel „terhelt”, vagy anélküli tájra vonatkoznak.
4.A tájökológiában vagy a mátrix, vagy a folyosók konnektivitásáról beszélhetünk (Forman, 1995), a szoftveres tájmetriai feldolgozás során azonban éppen ezeket nem tudjuk figyelembe venni. Létezik külön alkalmazás a folyosók konnektivitásának a mérésére is, most azonban csak a foltokból összeálló ökológiai folyosóhálózat (lépegető kövek, stepping stones) elméletére épül. A konnektivitás a fajok lehetőségét jelenti a tájelemek elérésére (Báldi, 1998), azaz nem követünk el nagy hibát, ha fajonként definiáljuk azt a minimális távolságot, amit egy faj biztosan megtesz azért, hogy eljuthasson a következő foltig és ha a foltok ezen a távolságon belül vannak, akkor beszélünk azok összekötöttségéről, összekapcsoltságáról (ez voltaképpen csak nevezéktani probléma, mivel a nem folytonos folyosók esetében is át kell hidalniuk a fajoknak a távolságot a továbbhaladáshoz).
A mérőszámok sokfélesége miatt most csak néhány példát mutatunk be. Bővebben lásd Szabó (2009) munkájában, ahol módszertani szempontból kerültek jellemzésre az indexek.
A kiindulási alapunk egy raszteres, vagy vektoros fedvény, mely a felszínborítási kategóriákat tartalmazza. A feldolgozás folt szinten kezdődik, mivel számos index osztály és táj szinten a folt szinten mért értékek számtani, vagy súlyozott átlagából kerül kiszámításra.
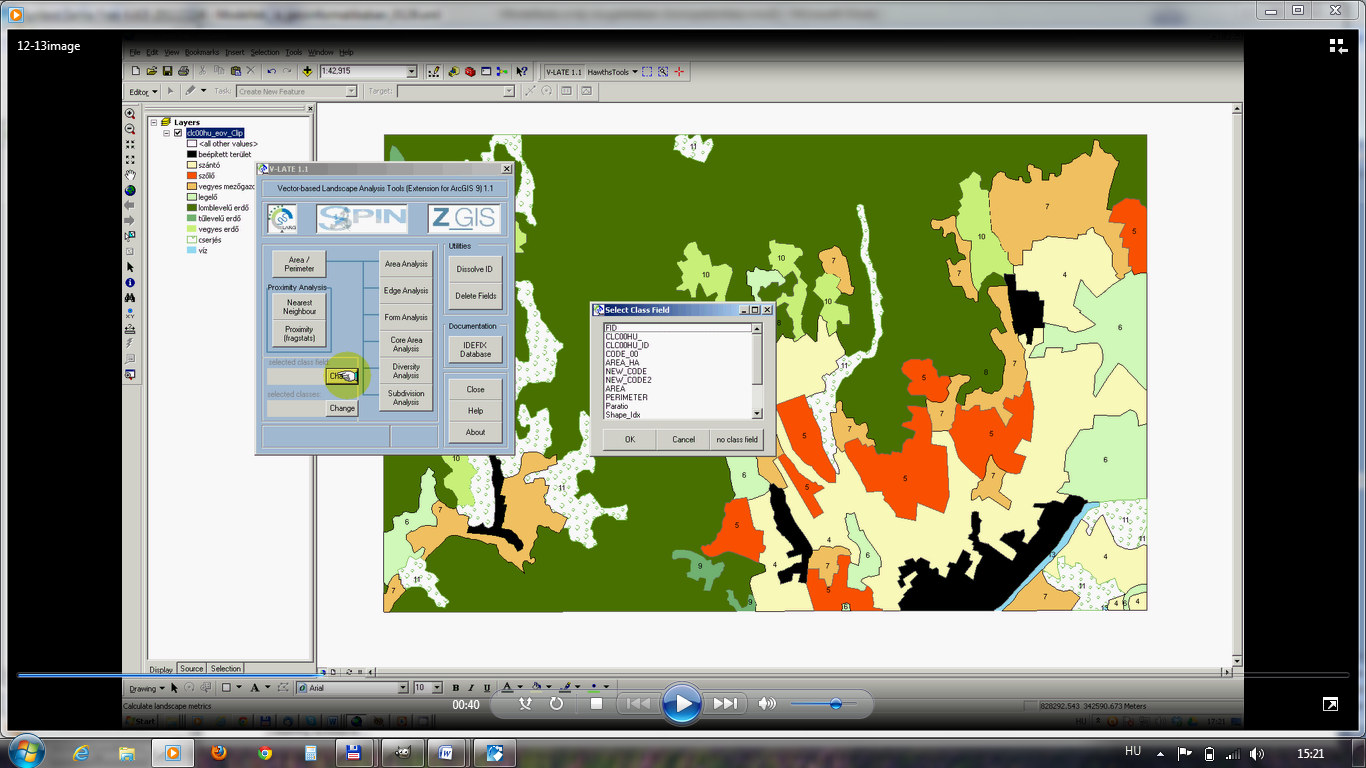
Példánkban egy zempléni tájrészlet tájmetriai mutatóit számítjuk ki a CLC2000 adatbázis kivágatán. A számításhoz az ArcGIS9 szoftverkörnyezetben futó vLATE bővítményt használjuk. A bővítmény használatához be kell állítanunk a fedvény vetületét, mely mindenképpen méter alapú koordinátarendszer kell, hogy legyen (esetünkben HD1972 EOV). Ezt követően futtatjuk a vLATE bővítményt, melynek egy olyan oszlopra van szüksége a táblázatban, ami megadja a felszínborítási kategóriákat (newcode2). Az eredeti CLC kategóriákat az egyszerűsítés miatt összevontuk és a számításokat ezekre végeztük el. Számítsuk ki a foltok területét, kerületét, valamint az alaki jellemzőket. A munka mentét lásd a 7.14. videóban.
7.14. ábra - Egy zempléni tájrészlet tájmetriai mutatóinak kiszámítása. A vLATE bővítmény használatának folyamata
 |
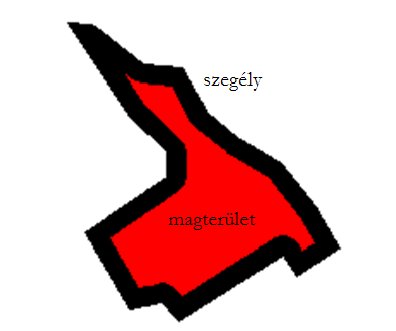
Az eredmények alapján ki tudjuk értékelni az adott tájrészlet foltjainak tulajdonságait. A foltméret (AREA) kérdése egyszerű: minél nagyobb foltról van szó, annál nagyobb a fajgazdagsága és mivel ezen foltoknak a belső zónája (magterület, CORE AREA) is nagy, az értékes, szűk ökológiai tűréstartományú fajok is meg tudnak telepedni. A foltalak (SHAPE, FRAC) a kontinensek tagoltságához hasonlítható, de értékelésénél a tagolatlan határvonalat tekintjük kívánatosnak: a megnyúlt, sok félszigetszerű kiágazással tagolt foltok fajgazdagsága a csökkenő belső terület miatt kisebb, egyes esetekben akár a belső zóna is teljesen hiányozhat (7.15. ábra). Ezek a foltok általában sérülékenyebbek is. (Itt jegyezzük meg, hogy a tájmetriai módszerek egy részénél nem ajánlott a térképről digitalizált fedvényeket elemezni, mivel a térképeken minden objektum körvonala generalizált, így a kerület, alak stb. nem a valós képet mutatja. A térképek célja az ábrázolt terület objektumainak a bemutatása, melyek generalizáltak és nem a valós képet adják vissza, hanem annak csak egy egyszerűsített változatát. Ha számunkra fontos a foltok alakja, akkor helyesebb légifotókat, műholdfelvételeket alkalmazni.)
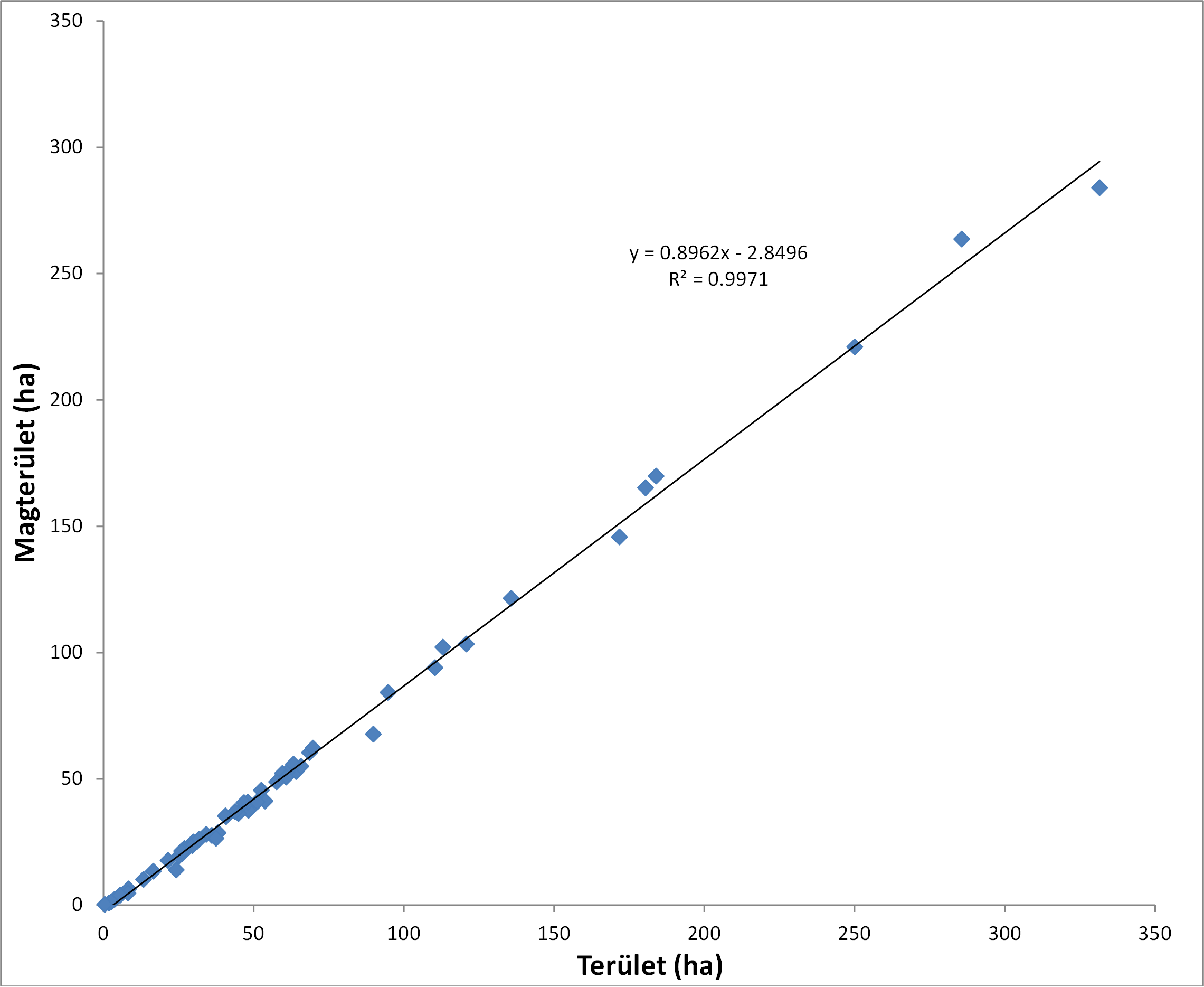
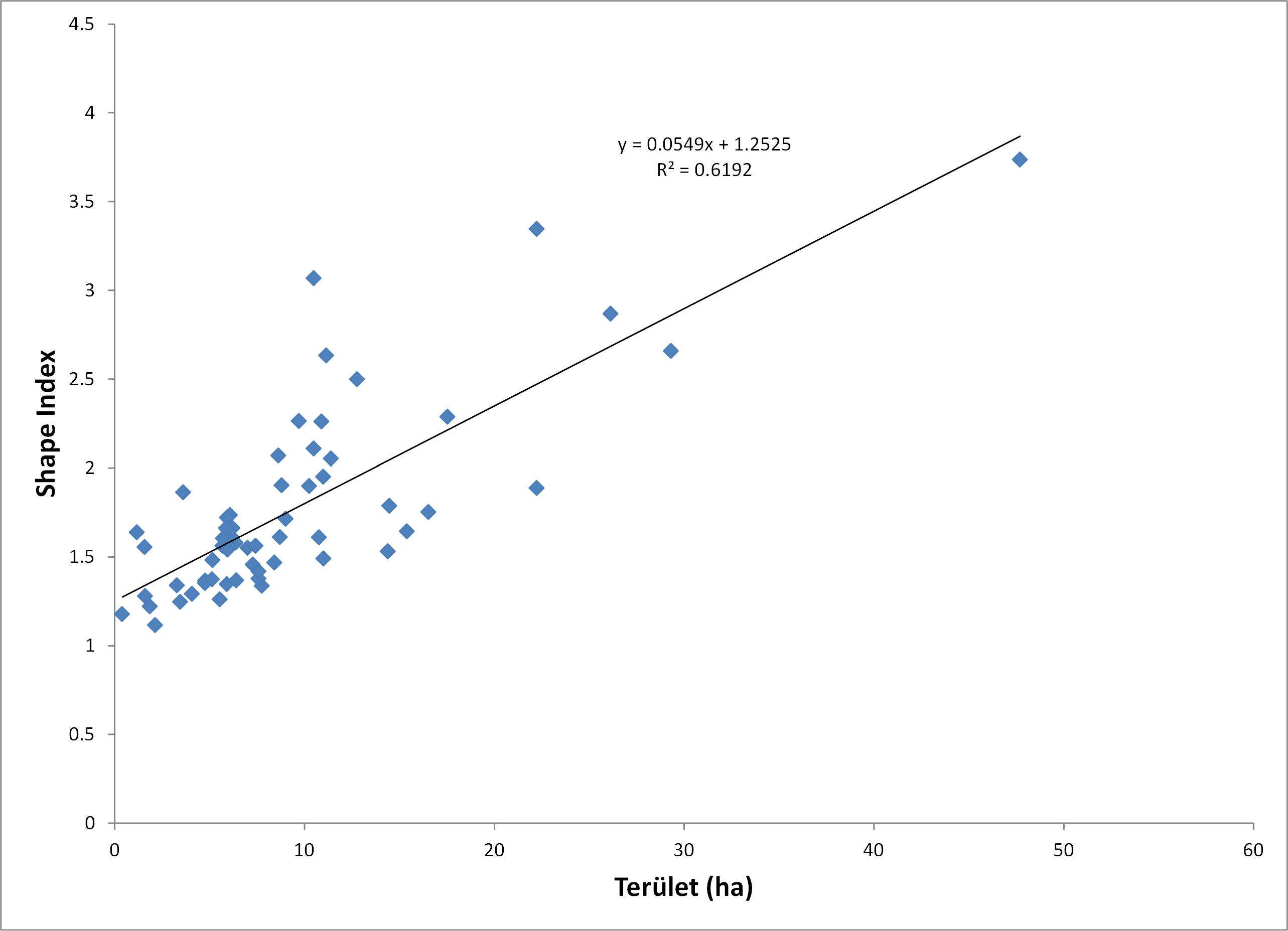
A kiértékeléshez egyszerű pontfelhő diagramot és lineáris regressziót használtunk. Eszerint mintaterületünkön igaz a korábbiakban feltételezett összefüggés a foltméret növekedése és a magterület növekedése között (a számítás során 30 m-es szegélyzónával kalkuláltunk). A kapcsolat igen szoros, a determinációs együttható (R2) értéke 0.99 (7.16. ábra). Esetünkben az is igaz, hogy a foltok mérete és alakja szintén pozitív korrelációs kapcsolatban van: minél nagyobb egy folt mérete, annál komplexebb a formája, vagyis a kisebb foltok (ez esetben legalábbis) kompaktabbak. A foltméret 69%-ban magyarázza az alaki mutató értékeinek a varianciáját (7.17. ábra).
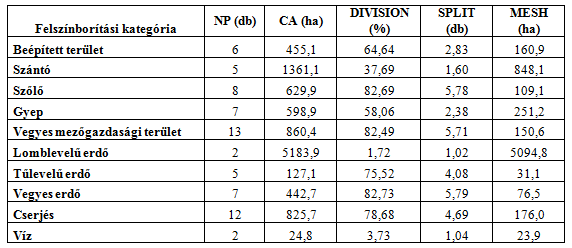
Az osztály szintű mutatók alkalmasak a táji mintázatok vizsgálatára. A fragmentáció, a foltok elhelyezkedése egymáshoz képest, valamint konnektivitásuk az ökológiai, tájökológiai kutatások egyik kulcskérdése. A foltok fragmentációját szintén a vLATE bővítménnyel határoztuk meg. Ezen mutatókat osztály szinten értelmezzük, mivel ez esetben a célunk az egyes felszínborítási kategóriák konnektivitási és fragmentáltsági tulajdonságainak az értékelése. A bővítmény a Jaeger (2000) által kidolgozott fragmentációs indexeket és a foltok számát számítja ki. Jaeger felosztottsági (subdivision) mutatóknak hívja összefoglaló néven az általa kifejlesztett indexeket (MESH, SPLIT és DIVISION), melyek abból indulnak ki, hogy két véletlenszerűen elhelyezkedő állat helyzetének valószínűsége meghatározható arra nézve, hogy ugyanabban a tájfoltban legyen a vizsgálati területen, ami pedig a táj felosztottságának a függvénye.
-A DIVISION index azt adja meg, hogy mekkora a valószínűsége annak, hogy a vizsgálati területen véletlenszerűen elhelyezkedő két állat NEM ugyanazon a folton található meg.
-A SPLIT (Splitting Index) azt adja meg, hogy hány részletre kell vágni a tájat ahhoz, hogy a fenti valószínűség állandó maradjon.
-a MESH azt adja meg, hogy mekkora az előző mérőszámban meghatározott darabszámból következő egyforma méretű területek nagysága.
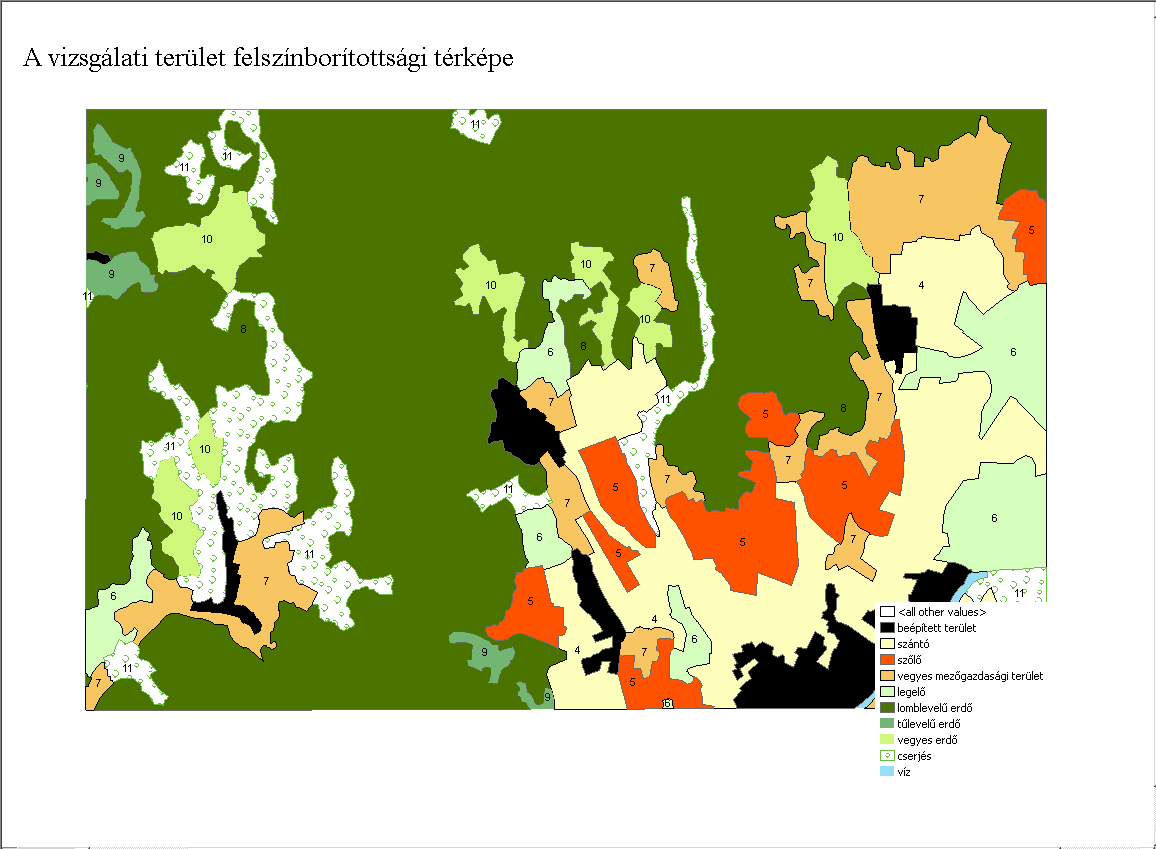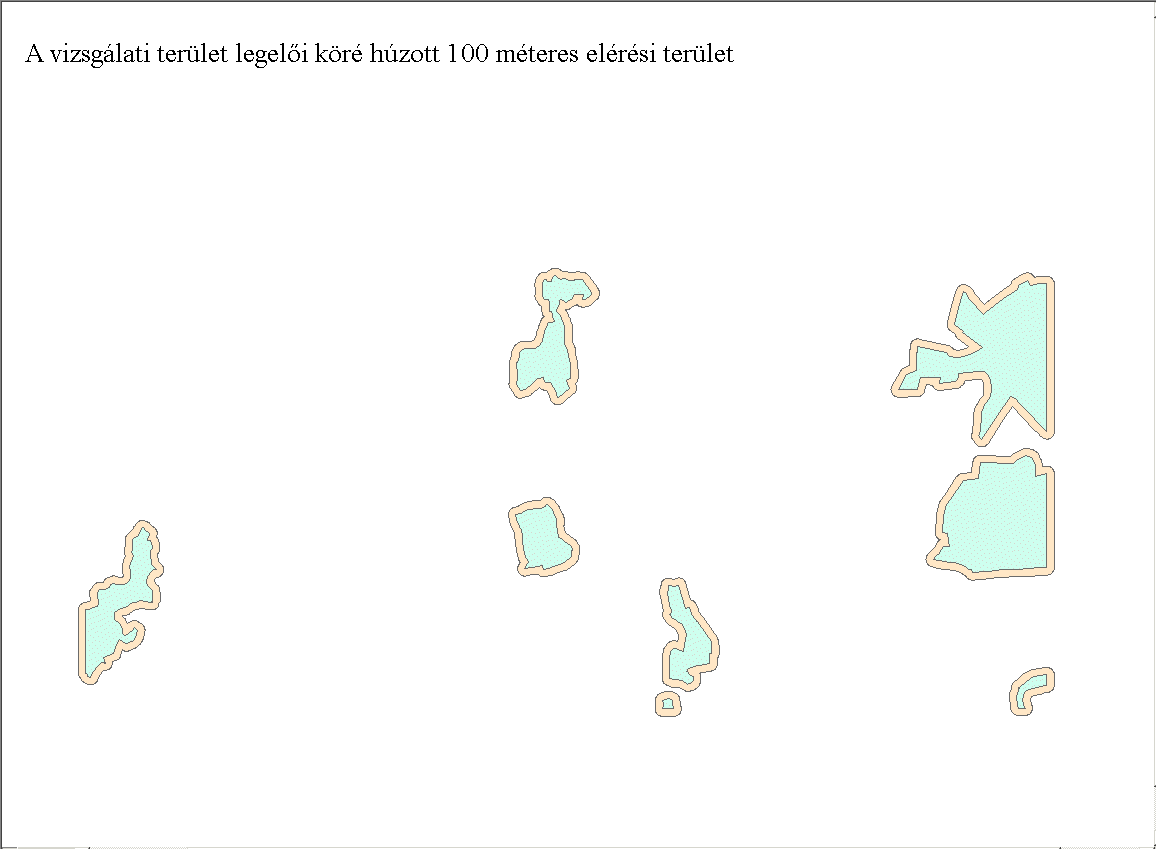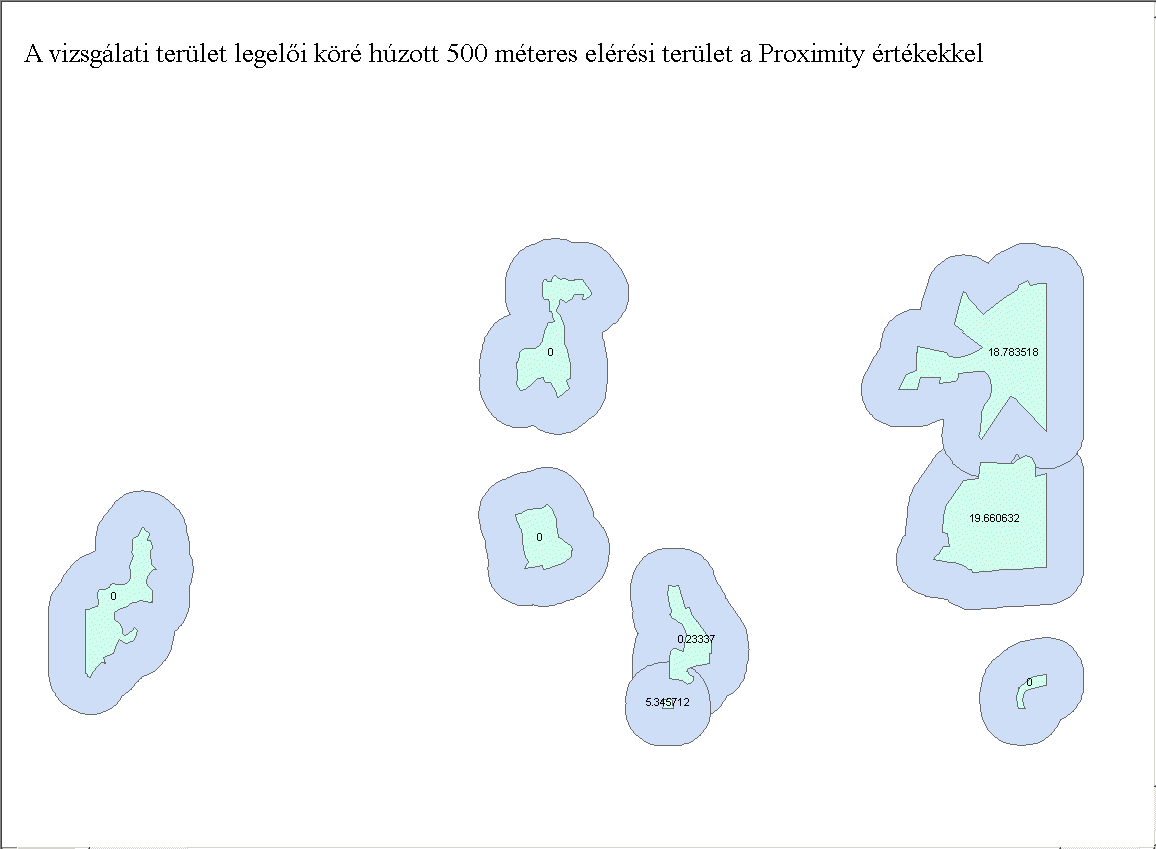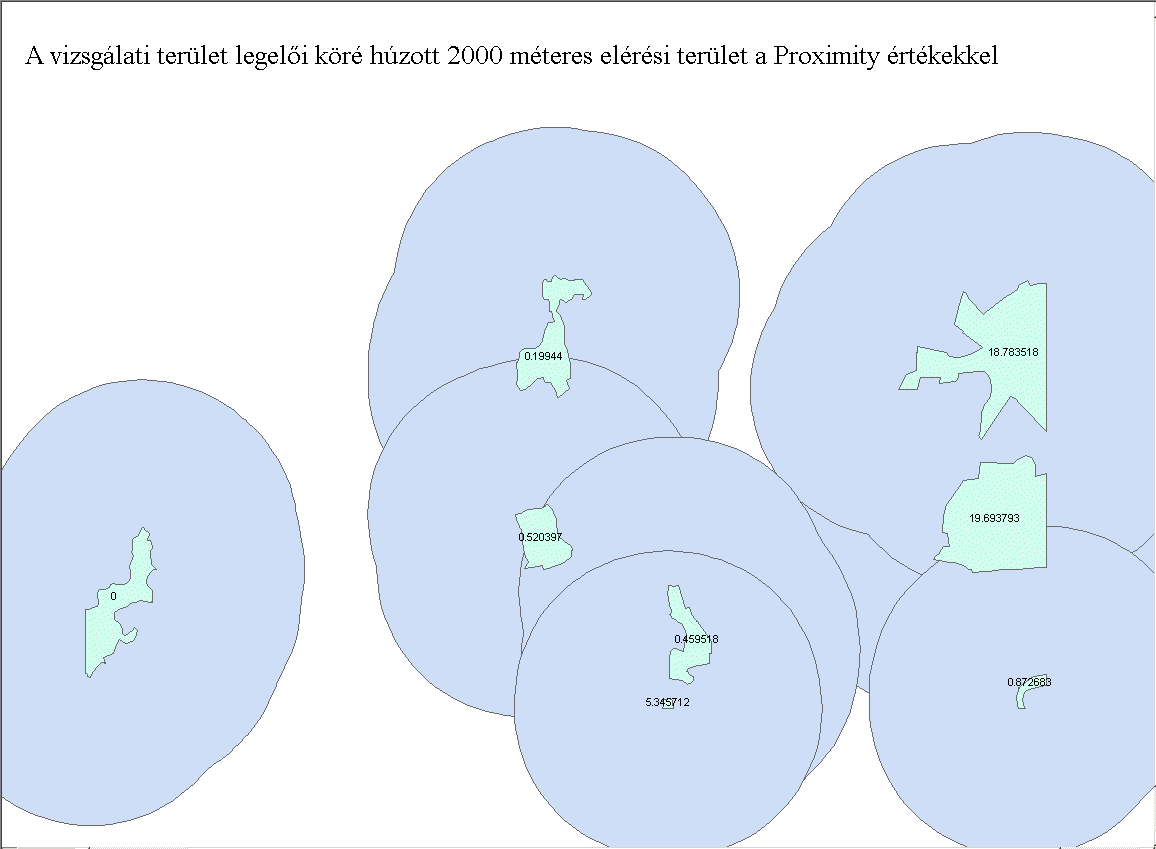
Vizsgálati területünkön az erdő (11-es kategória) a legkevésbé fragmentált, míg a szőlő, vegyes erdő és cserjés (sorrendben: 5, 10 és 11-es kategóriák) a leginkább felszabdaltak (7.18. ábra). Az eredmények interpretálásánál fontos figyelembe venni, hogy valóban felszabdaltságról van-e szó, vagy ez a természetes megjelenése a foltoknak az adott tájban. További lehetőség az azonos kategóriába tartozó foltok távolságának a meghatározása euklédeszi távolságként (NNDist, Euclidean Nearest Neighbour Distance). A meghatározás folt szinten történik (méterben), de kategóriánként átlagot, szórást számíthatunk az oszlopokból. További lehetőség a Proximitiy Index kiszámítása (7.19. ábra). Meg kell adnunk egy elérési távolságot (amit egy faj hajlandó megtenni/meg tud tenni ahhoz, hogy elérje a következő élőhely foltot) és a program azt fogja meghatározni, hogy ezen a távolságon belül átlagosan mekkora terület esik belül (7.20. ábra).