Térképeket nemcsak kategóriánként (nominális adatokként) hasonlíthatunk össze, sokszor metrikus adatok jelentik a pixelekhez tartozó értékeket. Ilyenkor a képek közötti korrelációt számítjuk ki. A Pearson-féle korrelációs koefficienst, illetve regresszió alkalmazásakor a determinációs együtthatót határozzuk meg. A két vizsgálatba vonható változó lehet pl. 2 különböző időpontból származó NDVI fedvény, ahol a két térkép hasonlóságát kapjuk meg (minél nagyobb a korreláció, annál jobban hasonlítanak), de lehet pl. az agyagtartalom és a kémhatás fedvénye is, ahol a két fedvény kapcsolatát határozzuk meg (regresszió, az R2 megadja, hogy az agyagtartalom hány százalékot magyaráz a kémhatás varianciájából).
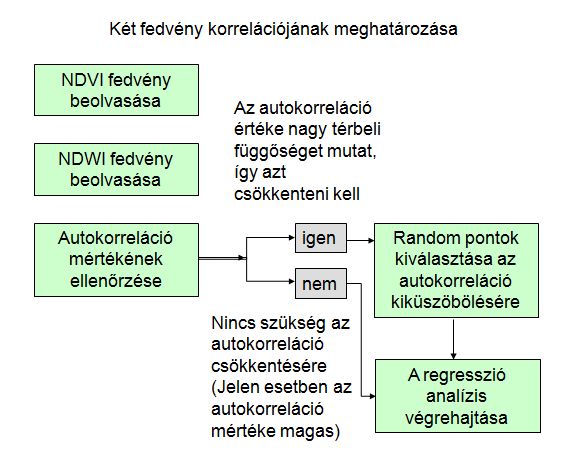
A regresszió alkalmazásának fontos előfeltétele, hogy biztosítsuk az adatok függetlenségét, mivel sokszor interpolált térképekkel dolgozunk, ahol magas az autokorreláció (térképek esetében a térbeli függőség). Mivel raszteres fedvényekről van szó, az elemszám kellően magas marad akkor is, ha a pixeleknek csak 10-20%-át használjuk fel egy random mintavételezés után. Így mivel nem egymás melletti pixelekből áll össze a adatmátrixunk, a függetlenség feltételének is eleget teszünk.
Példánkban a Tisza-tó térségére kiszámítottunk két széles körben használt spektrális indexet, az NDVI-t (Normalized Difference Vegetation Index) és az NDWI-t (Normalized Difference Water Index) és megnézzük, hogy értékeik korrelációs kapcsolatban állnak-e egymással (7.13. ábra).