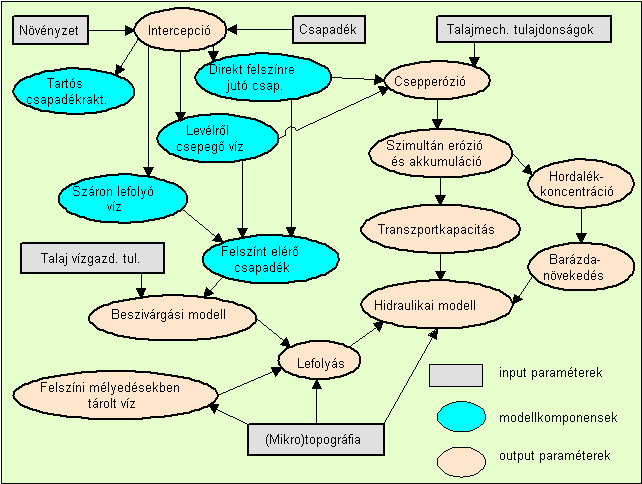
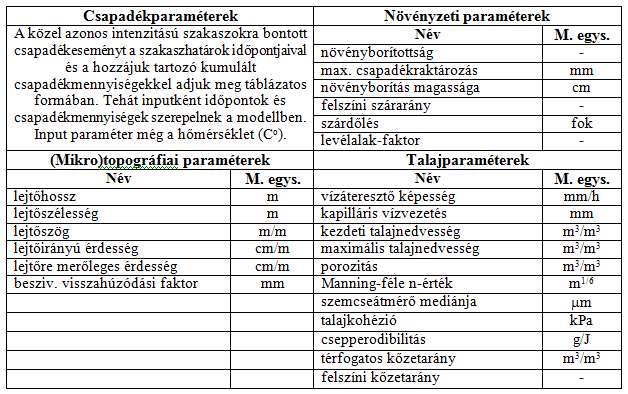
Több évtizedes kísérletezések, próbálkozások, majd szisztematikus méréssorozatok eredményeképpen született meg a ma már USLE néven közismertté vált „Egyetemes Talajvesztési Egyenlet” (Universal Soil Loss Equation) végleges formája (WISCHMEIER et al. 1978). A később számos eróziós modell alapjául is szolgáló USLE tulajdonképpen az első használható talajeróziós modell, hiszen eleget tesz az előző fejezetben megfogalmazottaknak.

Legfőbb ismérvei az alábbiakban foglalhatók össze:

- az eróziót alapvetően az esőenergia alapján határozza meg,

- az esőenergiából nagyszámú mérés alapján felírt tapasztalati képletekkel számolja az eróziót, azaz tapasztalati modell,

- parcellára, illetve mezőgazdasági táblára alkalmazható,

-az éves talajpusztulás mértékét adja meg t/ha-ban az adott éghajlati viszonyok között,

-statikus modell, tehát az erózió időbeni lefolyásáról nem szolgáltat információt.

A hiányosságokkal és korlátokkal terhelt USLE továbbfejlesztése nem váratott sokáig magára. Elsőként az egyes faktorok módosításával alkalmassá tették a modellt az egyedi csapadékesemények eróziós hatásainak a jellemzésére is, megalkotva a MUSLE-t (Modified Universal Soil Loss Equation). További jelentős módosítások után a modell már nemcsak szántóföldekre, hanem legelő- és erdőterületekre is alkalmazhatóvá vált (RUSLE – Revised Universal Soil Loss Equation). A még mindig USLE-alapokon nyugvó EPIC (Erosion Productivity Impact Calculator) modell kidolgozásának célja a farmerek számára egy olyan kis hardver- és szoftverigényű, könnyen kezelhető modell létrehozása volt, amely a vízerózió becslésén túl a szélerózió becslésére is alkalmas, és ezek alapján a terméshozamokat is előrejelzi. Segítségével a területhasznosítás optimalizálása is megoldható. Outputjai között szerepel pl. a lefolyás, az evapotranszspiráció, a talajvízszintváltozás is. Rendkívül sokoldalú használhatósága mellett továbbra is tapasztalati és statikus maradt. A tapasztalati modellek rendkívül nagyszámú mérési szükséglete miatt a 80-as évek elejétől kezdődően helyettük a dinamikus fizikai modellek ugrásszerű elterjedését figyelhetjük meg. Az utóbbi 30 évben több tucat eróziós modell látott napvilágot, amelyek közül a fontosabbak jellemzőit a 4.6. ábrán foglaltuk össze.

4.6. ábra - A fontosabb fizikai / elméleti modellek áttekintése (MORGAN, 1996, a web-oldal és a feltüntetett források nyomán)

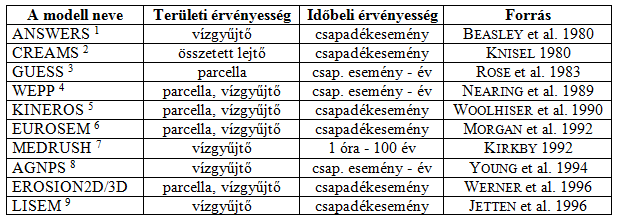¹Areal Nonpoint Source Watershed Environment Response Simulation, ²Chemical Runoff and Erosion from Agricultural Management System, ³Griffith University Erosion Sedimentation System, ⁴Water Erosion Prediction Project, ⁵Kinematic Runoff and Erosion Model, ⁶European Soil Erosion Model, ⁷Mediterranean Runoff Simulation on Hillslopes, ⁸Agricultural Non-Point-Source Pollution Model, ⁹Limburg Soil Erosion Model

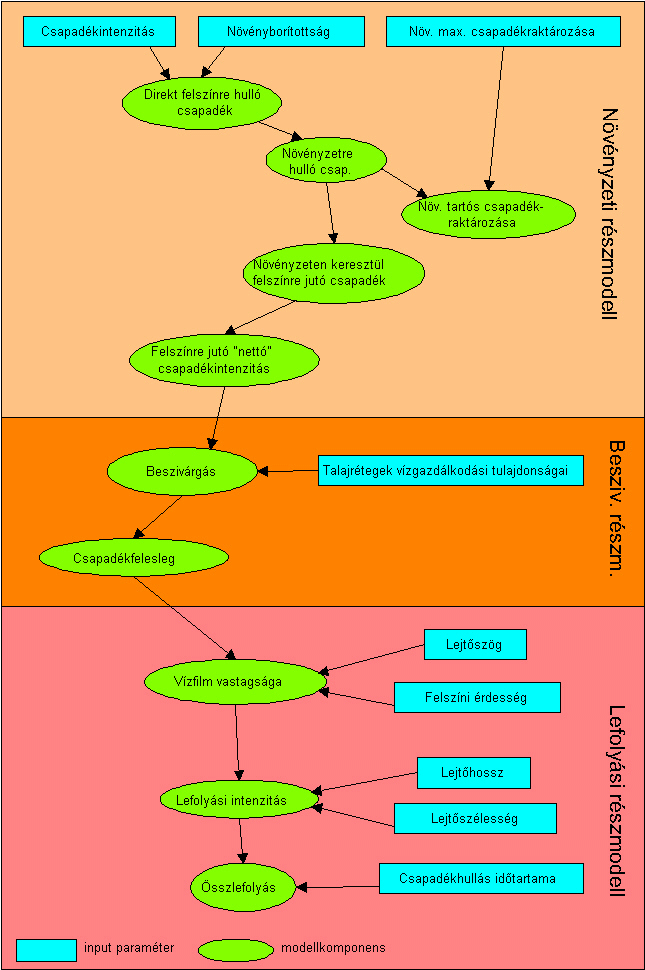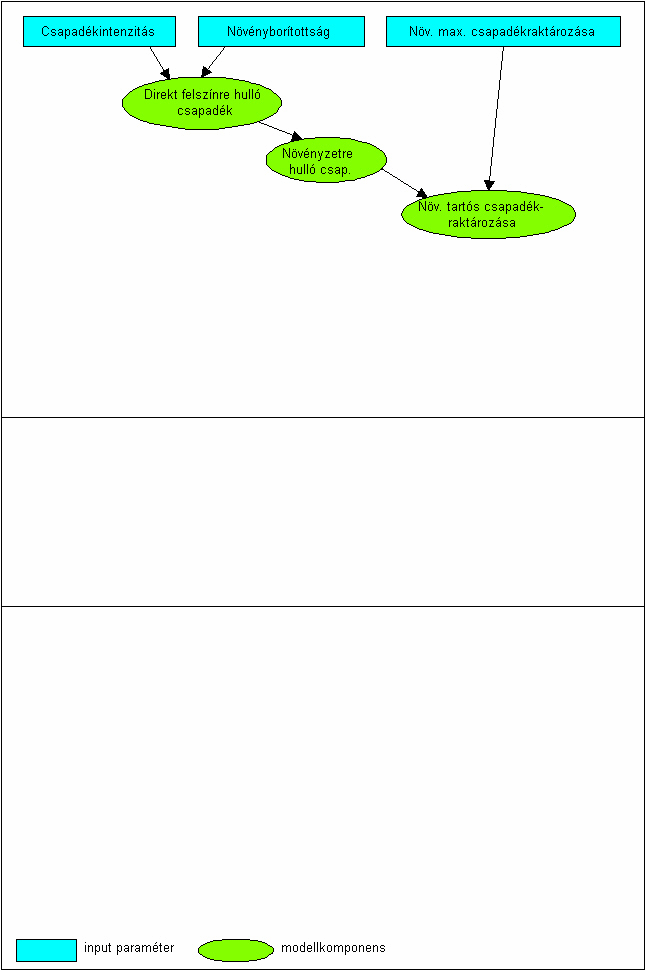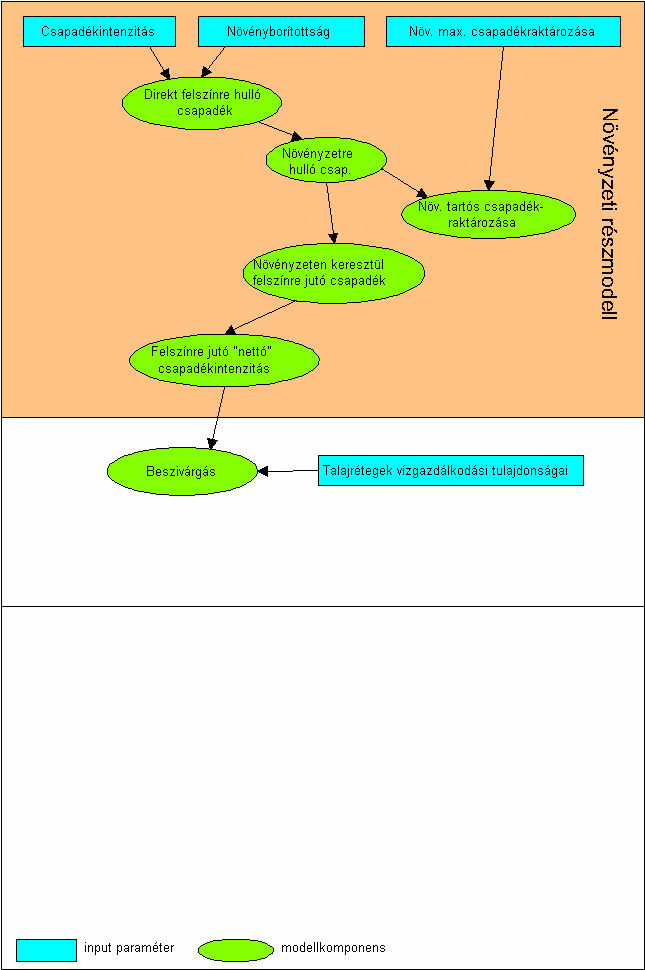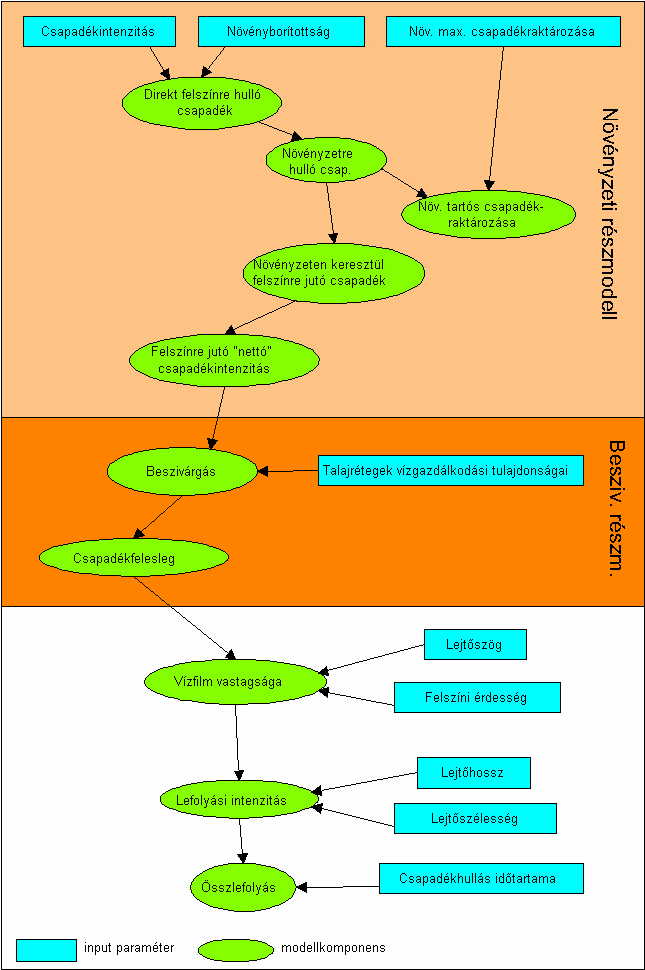
A felsorolt fizikai és elméleti modellekre jellemző, hogy a lefolyást és az eróziót már képesek külön kezelni, többségük kétváltozós differenciálegyenletek segítségével írja le a lejtőmenti lefolyást (4.7.ábra), majd a csepperózió és a lefolyó víz hordalékszállítási dinamikájának matematikai leírásával határozza meg a talajveszteséget. A modellek egyik legfontosabb kulcskérdése a beszivárgás alakulása, mely alapvetően a fizikai talajféleségtől függ, és időbeli lefolyását a Green-Ampt-modell vagy a Horton-képlet alapján adja meg a legtöbb modell (MORGAN, 1996) (4.8. ábra, 4.9.ábra).

4.7. ábra - A fizikai modellek már nemcsak a mérési tapasztalatokon alapulnak, hanem a folyamatok dinamikáját írják le a csapadék-, a növényzeti és a talajjellemzők függvényében. Az animáció egy általános sémát mutat a modellek algoritmusára a csapadékhullástól a lefolyásig.

4.8. ábra - A beszivárgás alakulása az idő függvényében a hortoni modell szerint A: magas, de gyorsan csökkenő víznyelés szakasza; B: lassuló beszivárgás szakasza; C: állandósuló vízáteresztés szakasza; D: felszíni tócsaképződés kezdete; E: lefolyás kezdete K(t): víznyelő-vízáteresztő képesség időbeni alakulása (mm/h vagy mm/min) Ks: telített talaj vízvezető képessége (mm/h vagy mm/min) a, b: talajra jellemző paraméterek

4.9. ábra - Az interaktív animáció lehetőséget biztosít a fizikai féleségtől és egyéb talajjellemzőktől függő víznyelő-vízáteresztő képesség szimulálására, ld. még 4.8. ábra)

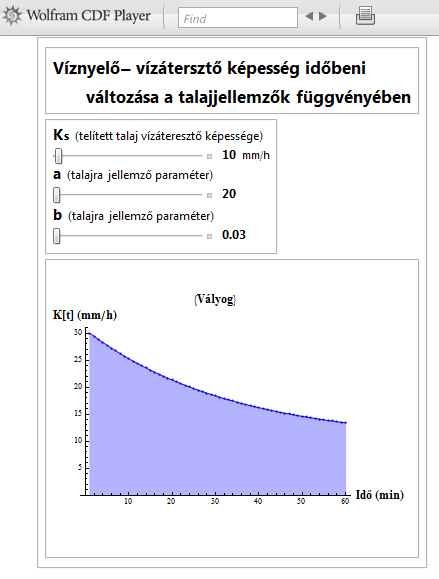A felsorolt vízeróziós modellek közül az alapvetően parcellákra kidolgozott EUROSEM-et és a GIS-alapú EROSION3D-t mutatjuk be.

4.3.1. Az EUROSEM modell összefoglaló jellemzése

A EUROSEM (European Soil Erosion Model) talajeróziós modellt a 90-es évek elejére dolgozták ki az Egyesült Királyságban, Silsoe-ban a University of Cranfield kutatóinak vezetésével. Létrejöttében nagy szerepet játszott a 80-as évek második felében megerősödő „modellgyártási hullám”, a megalkotása idején azonban már működtek a CREAMS és a WEPP modellek. Ezen modellek azonban csak statikus outputtal rendelkeznek, azaz csak a vizsgált területről távozó vízmennyiséget és talajveszteséget adják meg, továbbá számos olyan bemeneti paraméterrel dolgoznak, amelyek csak közvetett hatással vannak az erózióra (pl. evapotranszspiráció). Emiatt az európai országokban, ahol általában az éves talajveszteség döntő többségét egy-két nagyobb csapadékesemény okozza, alkalmazásuk nem szerencsés. Ezért az Európai Közösség 1986-os brüsszeli tanácskozásán létrehoztak egy talajeróziós szakemberekből álló kutatócsoportot, amely célja az alábbi követelményeknek megfelelő talajeróziós modell (4.10. ábra) megalkotása volt:

1. alkalmas legyen az európai országok fent említett viszonyai között az erózió becslésére és előrejelzésére, azaz

2. egyeseményes dinamikus modell legyen,

3. az eseményen belül is képes legyen a lefolyás és a hordalékmozgás időbeni jellemzésére,

4. viszonylag kevés, csak egy-egy csapadékesemény során az erózióra direkt hatást gyakoroló input paramétereket használjon,

5. egyeseményes dinamikus modell legyen,

6. parcellákra, mezőgazdasági táblákra és kisebb vízgyűjtőkre is alkalmazható legyen.

4.10. ábra - A EUROSEM modell működési mechanizmusa (MORGAN et al. 1998 alapján)

Az egyes bemeneti paramétereket a 4.11. ábra foglalja össze.

4.11. ábra - : A EUROSEM-ben használt legfontosabb input paraméterek

Az egyes tényezők közötti összefüggéseket nem tapasztalatokra alapozva, hanem fizikai törvényekkel írja le a modell, azaz a hátterét egzakt matematikai egyenletek adják.

Az eddig leírt struktúra homogén parcellákra és mezőgazdasági táblákra alkalmazható. Ezeket a homogén, minden paraméterében egységes területeket a modell „plane element”-eknek nevezi. Magyarul a tájföldrajzi eredetű, de a hazai talajeróziós szakirodalomban már használatos erotóp kifejezés alkalmazása javasolt. Mivel a modell fejlesztői nem kapcsolták a modellt semmilyen geoinformatikai rendszerhez, így kisvízgyűjtőkre történő kiterjesztése csak bonyolult topológia megadásával lehetséges:

1.A lineáris vízvezetést végző, barázdánál nagyobb méretű, önálló vízgyűjtővel rendelkező medrekre bevezették a „channel element” (mederegység) fogalmát, és az erotópokhoz hasonlóan paramétereket rendeltek hozzá. Természetesen ez új paraméterek alkalmazását is maga után vonta.

2.Ezek ismeretében a modellezni kívánt vízgyűjtőt felosztjuk erotópokra és mederegységekre.

3.A létrehozott egységek között topológiát definiálunk, melyben egyértelműen meghatározzuk az egységek közötti hidrológiai kapcsolatokat (kimondatlanul itt deklaráljuk, hogy a modell konvergens lefolyással dolgozik, azaz bármelyik egység csak egy egységnek adhatja tovább a vizét), és a térbeli elhelyezkedésüket (jobb- és baloldali egység megadása).

4.A modellt lefuttatjuk a topologikus egységekre.

A modell legutóbbi verziója 2010-ben jelent meg, és az alábbi honlapról bárki számára ingyenesen letölthető.