A modellnek, akár gyakorlati, akár elméleti felhasználásra kerül, tesztelhető kimenetet kell szolgáltatnia. A számítógépes modellek, mivel a kvantitatív modellek családjába tartoznak, szükségszerűen numerikusak vagy logikaiak, így véges kimenetet eredményeznek minden futtatáskor. A legtöbb esetben ezek az előrejelzések számszerűen összehasonlíthatók a valós mérésekkel (amelyeknek függetleneknek kell lenniük a modellalkotásnál felhasznált adatoktól), így a modell nagyon pontos teljesítményvizsgálata végezhető el. A modell outputból egy kevésbé precíz − de nem feltétlenül „rossz” − szinten kvalitatív következtetéseket is levonhatunk. Valójában, amikor a modellnek sztochasztikus eleme is van, akár a folyamatok, akár az input konstansok között, a numerikus eredmény kevésbé lesz jól meghatározott, így a modellek egy folytonos sorozata építhető fel az egyértelmű kimenettel rendelkező szigorúan determinisztikus kvantitatív modellektől, a többé-kevésbé valószínű outputtal bíró sztochasztikus modellek sorozatán keresztül, a teljesen kvalitatív modellekig, mint többek között a természeti földrajz tradicionálisan sikeres modelljei közé tartozó Davis ciklustana.
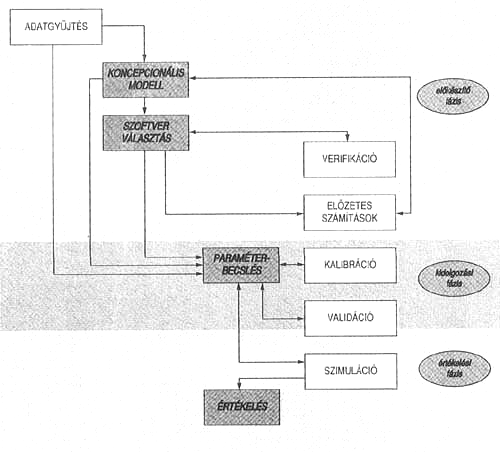
A számítógépes modellek használata során a következő nélkülözhetetlen lépések során juthatunk el a szimulációig (1.5. ábra):
1.Verifikáció: a verifikáció során arról kell meggyőződnünk, hogy egyszerű, általában analitikusan is megoldható esetekben a modell kielégítő megoldást szolgáltat-e. Erről leggyakrabban a modell dokumentációjából tájékozódhatunk.
2.Számítási háló meghatározása: a számítási háló meghatározza az elérhető pontosságot, és numerikus modellek esetében a futási időt is. Nagyobb felbontású, sűrűbb háló esetében pontosabb, részletesebb kimeneti adatbázist kaphatunk, viszont a futási idő indokolatlanul megnőhet. A számítási háló meghatározásában segítségünkre lehetnek az érzékenységi vizsgálatok.
3.Paraméterek megadása: a modell számára a szükséges paraméterek megadását jelenti. Modelltől függően kötelező minden paraméter megadása, vagy egyeseket akár el is hagyhatunk. Értéküket gyakran csak becsléssel tudjuk meghatározni.
4.Érzékenységi vizsgálat és kalibráció: a „trial and error” érzékenységi vizsgálat során arra keressük a választ, hogy bizonyos paraméterek értékeinek +- 10%-os változtatása milyen mértékű változást generál a modell által szolgáltatott eredményekben. A modellek egyes paramétereik értékének változására jobban, másokra kevésbé érzékenyek. Ennek tudatában szükséges egyes paraméterek minél pontosabb megadása. A kalibráció során a terepen mért eredményeket hasonlítjuk össze a modell által szolgáltatottakkal.
5.Validáció: a kalibráció során fel nem használt események adataival futtatjuk a modellt, és vizsgáljuk a szimuláció és a terepi mérések eredményei közötti kapcsolatot.
6.Szimuláció: a kalibrált és validált modell alkalmas arra, hogy bizonyos tényezők hatását a többitől függetlenül vizsgáljuk, valamint eddig még be nem következett szituációk eredményeit elemezhetjük.