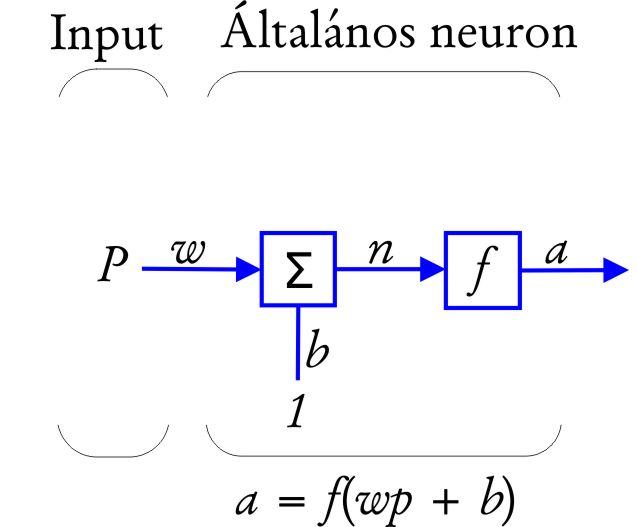
Az ANN-ok alapelemei az egyes neuronok (10.2 ábra). A bemenő p skalár és w súly, valamint a b bias (eltolás) és 1 konstans szorzatainak összege képezi a neuronba bejövő jel súlyozott összegének n értékét (net). A neuronba belépett, összegződött n értéket egy f aktivációs függvény alakítja át a kimeneti értékké (Paláncz, 2011). Az aktivációs függvény által átalakított jel adódik át a következő neuronnak (10.2. ábra).

10.2. ábra - Neurális hálózat sematikus működési modellje egy neuronnal és egy bemeneti jellel (Hagan et al. 1996 alapján)

10.3. ábra - Neurális hálózat sematikus működési modellje egy neuronnal és többszörös bemeneti értékkel (Hagan et al. 1996 alapján)

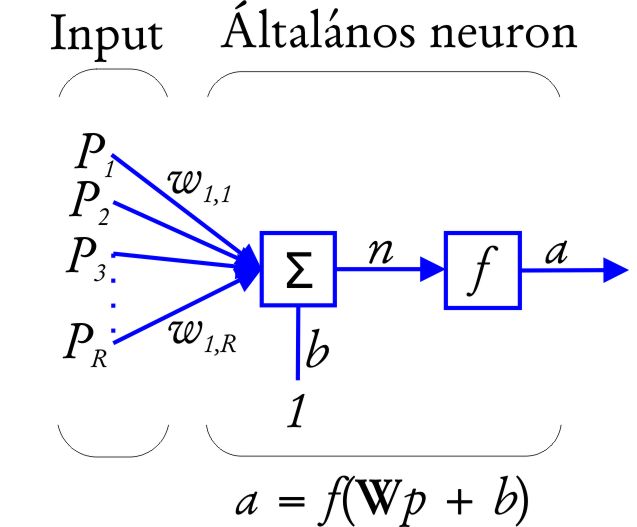Valójában a neuronoknak többszörös bemeneti értékei vannak (10.3 ábra). R különböző bemeneti érték esetén minden egyes p₁, p₂, …, p_R input a hozzá tartozó w_1,1, w_1,2, …, w_1,R súllyal szorzódik, ahol az első index a végponton lévő neuron sorszáma, a második a kezdő neuron sorszáma. A w_1,1, w_1,2, …, w_1,R súlyok képezik a w súlyvektort, az inputok vektora p . Ekkor a net inputot az n = w_1,1 p₁ +w_1,2 p₂+…+w_1,R p_R + b összeg adja, vagy vektoros formában: n = w•p+b.

A valós problémák megoldására általában nem elegendő egy neuron, hanem párhuzamosan dolgozó (azonos rétegen belül egymással kapcsolatban nem lévő) neuronokból álló rétegek kombinációjának eredményeként születő neurális hálózat szolgáltatja a megoldást (10.4. ábra). A legegyszerűbb ANN-ok egy bemeneti, egy rejtett és egy kimeneti réteget tartalmaznak (10.1. ábra). A bemeneti és kimeneti rétegek ismertek, míg a rejtett rétegeket ismeretlen értékű neuronok halmazai alkotják, amelyek nem állnak kapcsolatban a modell környezetével.

10.4. ábra - Neurális hálózat sematikus működési modellje két, S számú neuronból álló réteggel és többszörös bemeneti értékkel (Hagan et al. 1996 alapján)

10.5. ábra - Az első réteg súlymátrixa

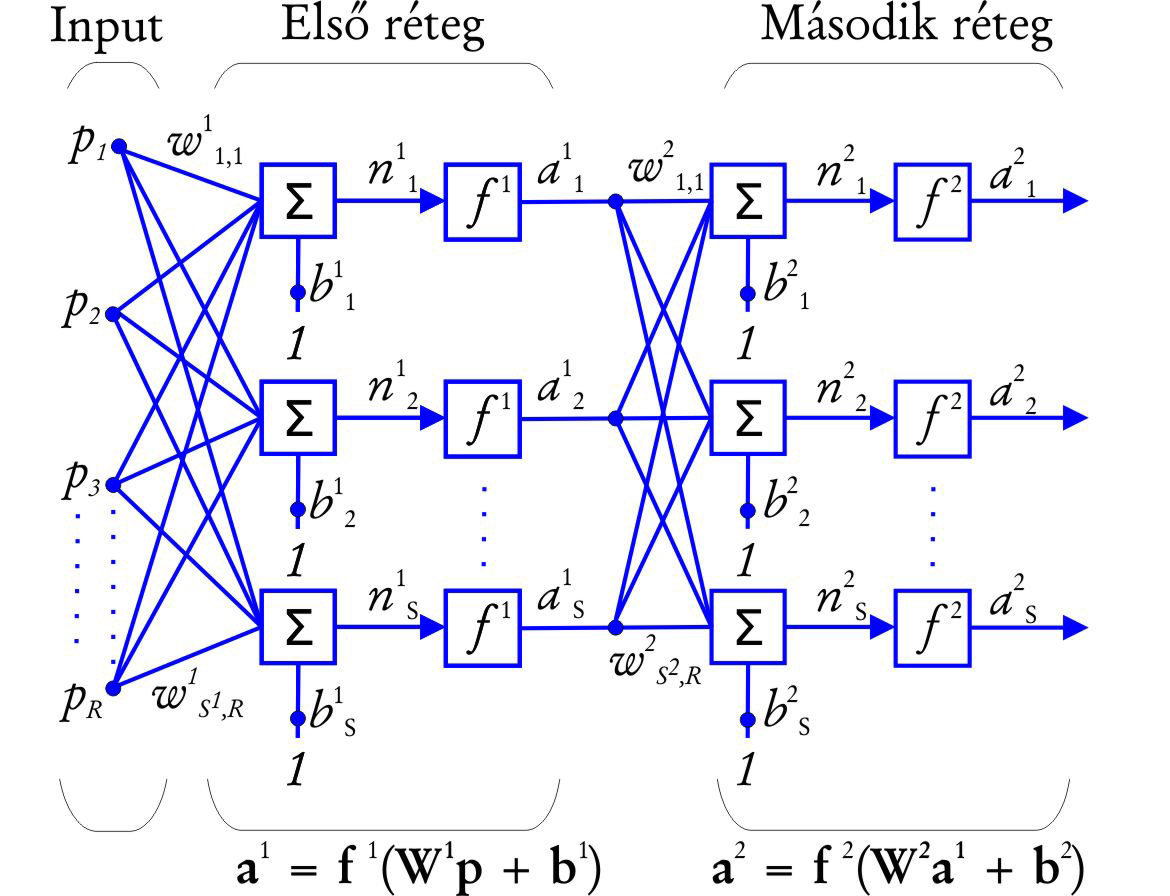Minden réteg saját aktivációs függvénnyel, súlymátrix-szal és bias-szal rendelkezik (10.5. ábra). A 10.4. ábrán az első réteg a rejtett, míg a második a kimeneti réteg. A második réteg (a² = f²(W¹a¹+b²) inputja az első réteg outputja. Így a hálózat outputját az a² = f²(W² f¹(W¹p+b¹)+b² összefüggés adja meg. A hálózat komplexitása és számítási képessége a rejtett rétegek és a rétegekben lévő neuronok számától függ.